实验目的

掌握R语言对数据集数据特征的分析方法

实验原理

对数据进行质量分析后，接下来可以通过绘制图表、计算统计量等手段对数据进行特征分析。

特征分析主要有分布分析、统计量分析、周期性分析、相关性分析等等

实验步骤

1、分布分析

分布分析可以揭示数据的分布特征和分布类型，对于定量数据，可以通过绘制频率分布直方图等可视化方法查看数据的分布情况；对于定性数据，可用饼图或条形图等方法查看分布情况。

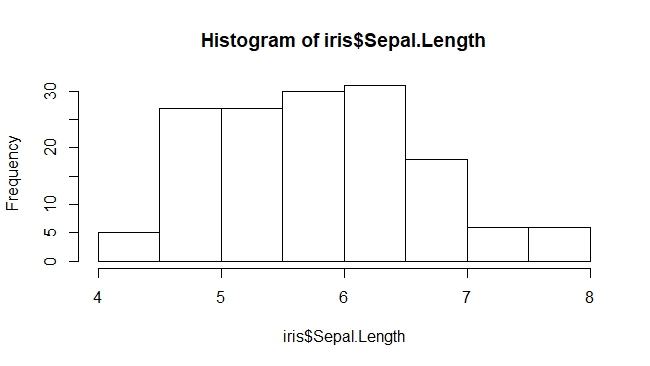
下面使用R语言中自带的数据集iris作为例子，对该数据集进行数据特征分析，首先对iris数据集中的Sepal.Length变量绘制直方图：

> hist(iris$Sepal.Length)

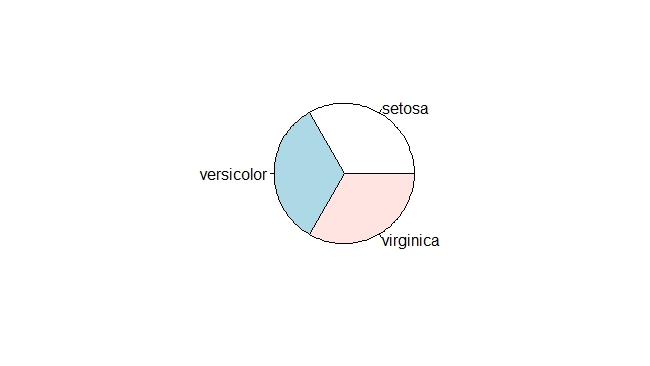
绘制iris数据集中变量Species的饼图

> table(iris$Species)
> pie(table(iris$Species))

2、统计量分析

用统计指标对定量数据进行统计描述，常从集中趋势和离中趋势两个方面进行分析。平均水平的指标是对个体集中趋势的度量，使用最广泛的是均值和中位数；反应变异程度的指标是对个体离开平均水平的度量，使用较广泛的是标准差(方差)、四分位数距。

R语言中summary()函数可以返回最小值、最大值、1/4分位数、3/4分位数、均值基本统计量：

> summary(iris)
  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width          Species  
 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100   setosa    :50  
 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300   versicolor:50  
 Median :5.800   Median :3.000   Median :4.350   Median :1.300   virginica :50  
 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199                  
 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800                  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500

另外var()函数可以返回方差，sd()函数可以返回标准差

> var(iris$Sepal.Length)
[1] 0.6856935
> sd(iris$Sepal.Length)
[1] 0.8280661

3、周期性分析

周期性分析是探索某个变量是否随时间变化而呈现出某种周期变化趋势。

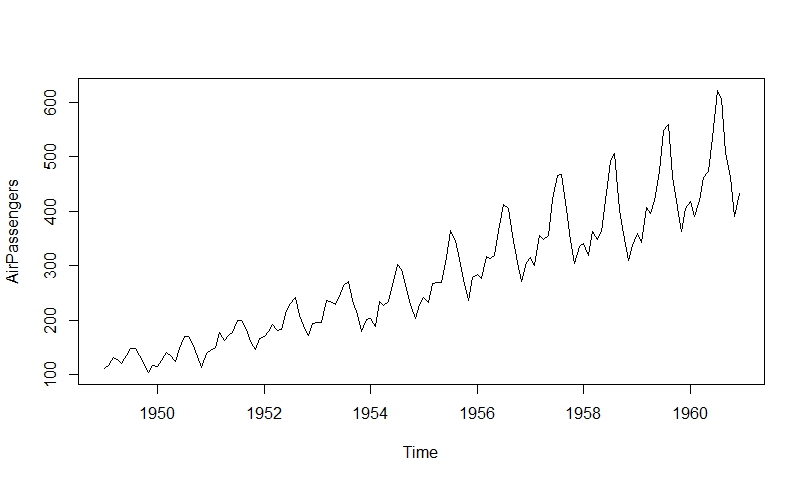
下图所示为1949年1月到1960年12月国际航班每月的乘客总数。从图中可以看出，每年的高峰期为7-8月附近，且年末有一个小峰，可能是因为放假，这种现象我们可以称为季节效应。此外，从总体发趋势来看，乘客总数随着年份稳定增长。

> plot(AirPassengers, main="每月乘客数量", xlab="时间", ylab="乘客数")

4、相关性分析

分析连续变量之间先行相关程度的强弱成为相关分析，进行相关分析可以通过绘制散点图、散点图矩阵、计算相关系数等方法。

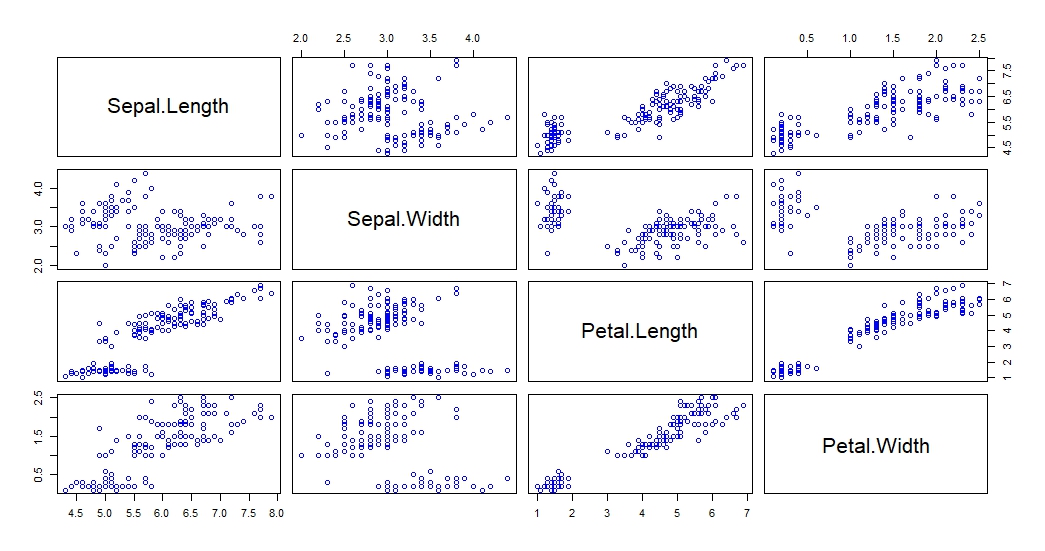
下例绘制iris数据集散点矩阵图，查看数据集中各变量关系

> pairs(iris[, 1:4], col = "blue")

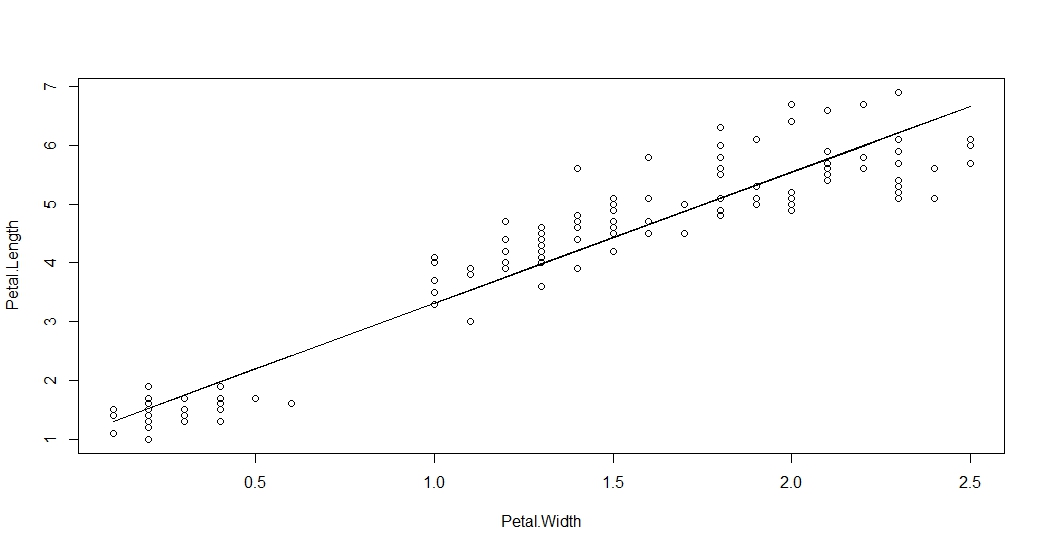
绘制Petal.Width和Petal.Length的散点图并添加回归线

> plot(Petal.Width, Petal.Length)
> lines(Petal.Width, lm1$fitted.values)

计算Petal.Width和Petal.Length的相关系数

> cor(iris$Petal.Width,iris$Petal.Length,method="pearson")
[1] 0.9628654

实验二：数据特征分析实验