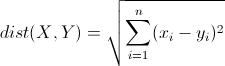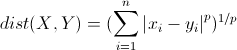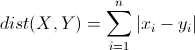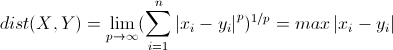实验一:KNN分类实验
一 实验目的
- 了解KNN算法的基本思想,学习基于实例的学习
- 了解KNN算法原理,优缺点以及使用技巧
- 学会使用R语言建立KNN分类模型
二 实验原理
KNN是k nearest neighbor 的简称,即k最邻近,就是找k个最近的实例投票决定新实例的类标。KNN是一种基于实例的学习算法,它不同于贝叶斯、决策树等算法,KNN不需要训练,当有新的实例出现时,直接在训练数据集中找k个最近的实例,把这个新的实例分配给这k个训练实例中实例数最多类。KNN也称为懒惰学习,它不需要训练过程,在类标边界比较整齐的情况下分类的准确率很高。KNN算法需要人为决定K的取值,即找几个最近的实例,k值不同,分类结果的结果也会不同。
基于实例的学习
存储所有实验用例,当有分类请求时,根据查询实例和已有实例的关系进行局部计算分类。不会有全局性的计算函数。归纳偏置是实例分布在欧式空间里是平滑的。
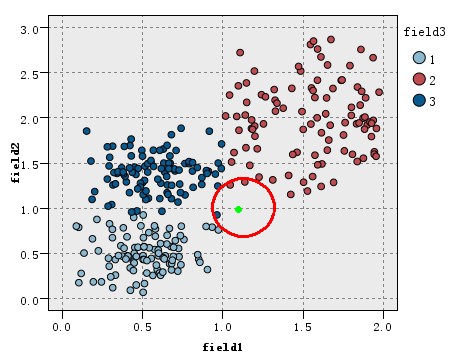
KNN简单例子:
看如下图的训练数据集的分布,该数据集分为3类(在图中以三种不同的颜色表示),现在出现一个待分类的新实例(图中绿色圆点),假设我们的K=3,即找3个最近的实例,这里的定义的距离为欧氏距离,这样找据该待分类实例最近的三个实例就是以绿点为中心画圆,确定一个最小的半径,使这个圆包含K个点。
算法:
训练样本是多维特征空间向量,其中每个训练样本带有一个类别标签。算法的训练阶段只包含存储的特征向量和训练样本的标签。在分类阶段,k是一个用户定义的常数。一个没有类别标签的向量(查询或测试点)将被归类为最接近该点的k个样本点中最频繁使用的一类。一般情况下,将欧氏距离作为距离度量,但是这是只适用于连续变量。在文本分类这种离散变量情况下,另一个度量——重叠度量(或海明距离)可以用来作为度量。
算法描述
1、计算已知数据集中的点与当前点的距离
2、按距离递增次序排序
3、选取与当前数据点距离最近的K个点
4、确定前K个点所在类别出现的频率
5、返回频率最高的类别作为当前类别的预测
距离度量:
距离度量(Distance)用于衡量个体在空间上存在的距离,距离越远说明个体间的差异越大。
- 欧几里得距离(Euclidean Distance):
明可夫斯基距离(Minkowski Distance):
曼哈顿距离(Manhattan Distance):
切比雪夫距离(Chebyshev Distance)
参数选择:
如何选择一个最佳的K值取决于数据。一般情况下,在分类时较大的K值能够减小噪声的影响,但会使类别之间的界限变得模糊,造成欠拟合。而较小的K值会过拟合。一个较好的K值能通过各种启发式技术来获取。在二元(两类)分类问题中,选取k为奇数有助于避免两个分类平票的情形。
三 实验步骤
第一步,获得数据并了解数据:
本教程将使用Iris数据集,这在机器学习领域是众所周知的。 此数据集内置在R中,因此您可以通过在控制台中键入以下内容来查看此数据集:
> str(iris)
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
> head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
通过summary命令,你可以大致了解数据的分布,summary为你提供数据集的基本统计信息,如下:
> summary(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:50
Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
在数据分析中,掌握必要的领域知识是很有必要的 :比如在iris这个数据集中,你要明白所有的花朵都包含萼片和花瓣。 萼片包围花瓣,通常是绿色和叶状,而花瓣通常是有色的叶子。 对于鸢尾花,这只是有点不一样,如下图所示: 了解领域知识能帮助你更好地做之后的特征工程。
了解领域知识能帮助你更好地做之后的特征工程。
第二步:进一步了解数据,可视化
首先,您可以通过制作一些图形(如直方图或boxplots)来尝试了解您的数据。 然而,在这种情况下,散点图可以让您很好地了解您正在处理的内容:可以看到有多少变量受到另一个变量的影响。换句话说,你想看看两个变量之间是否有任何关联。
换句话说,你想看看两个变量之间是否有任何关联。例如,您可以使用ggvis包进行散点图。多说一句,在使用ggvis包之前,你需要加载它。相关变量的选择同学可以自行选择,同时您也可以选择其他的可视化工具,如ggplot2。
#安装ggvis包
install.packages("ggvis")
# 加载`ggvis`
# 如果遇到缺少**包,安装解决
library(ggvis)
# Iris散点图
iris %>% ggvis(~Sepal.Length, ~Sepal.Width, fill = ~Species) %>% layer_points()
得到如下结果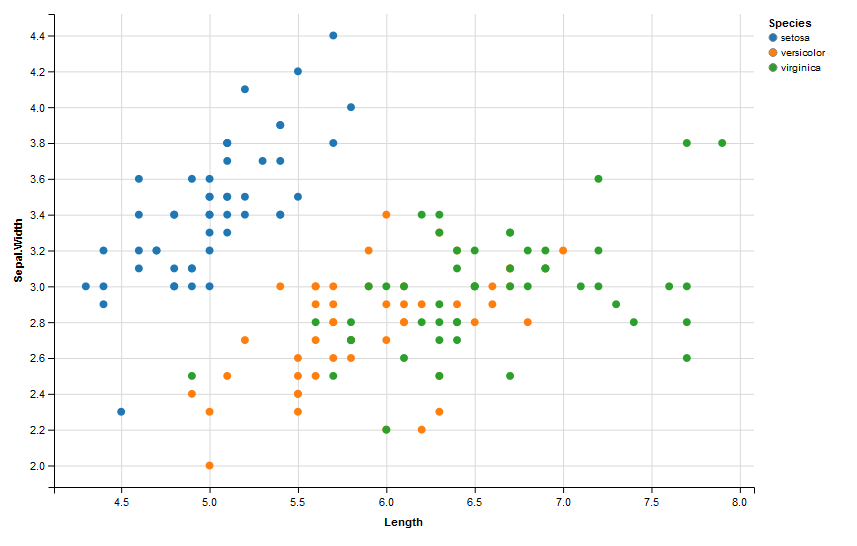
#安装kknn包
install.packages("kknn")
library(kknn)
data(iris)
m<-(dim(iris))[1]
val<-sample(1:m,size=round(m/3),replace=FALSE,prob=rep(1/m,m))
#建立训练数据集
data.train<-iris[-val,]
#建立测试数据集
data.test<-iris[val,]
#调用kknn 之前首先定义公式
#formula :Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width
iris.kknn<-kknn(Species~.,data.train,data.test,distance=1,kernel="triangular")
summary(iris.kknn)
# 获取fitted.values
fit <- fitted(iris.kknn)
# 建立表格检验判类准确性
table(data.test$Species, fit)
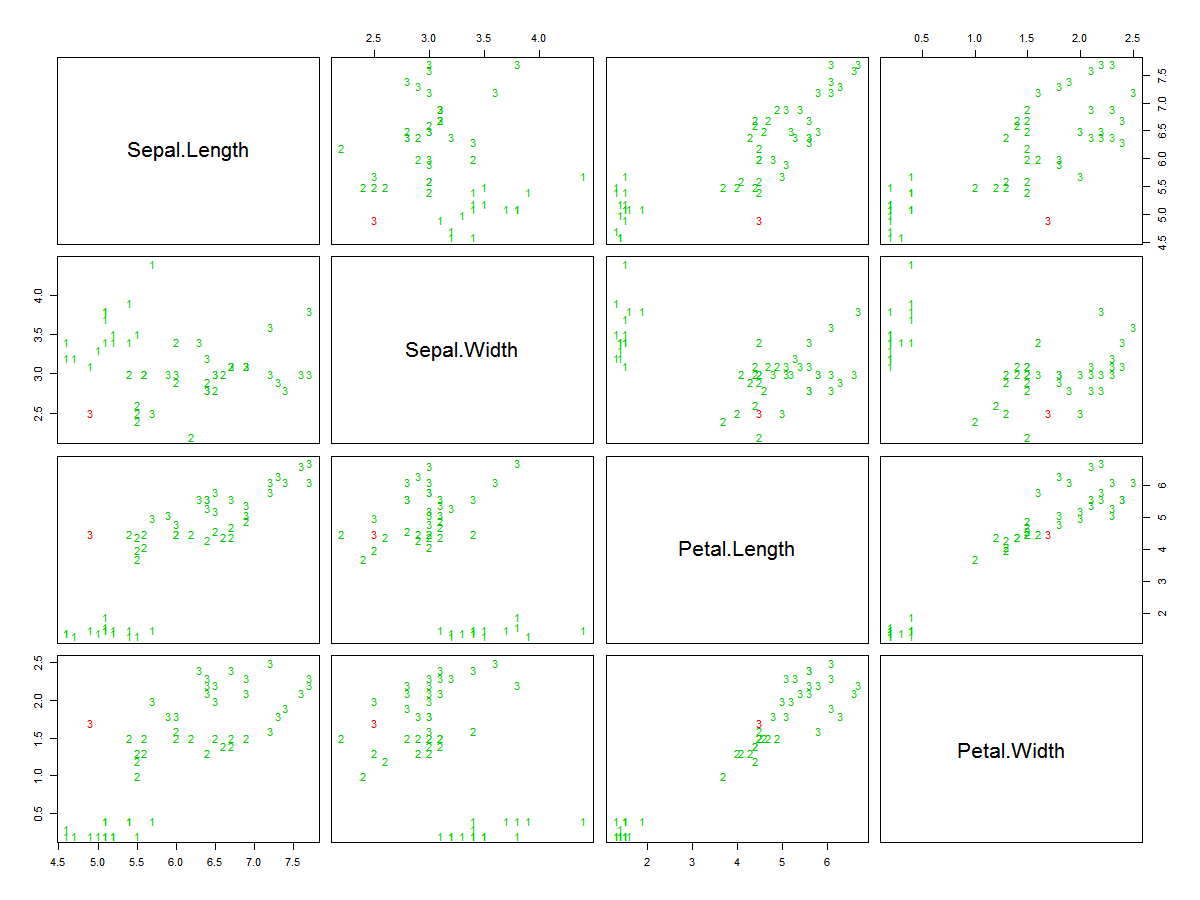
# 绘画散点图,k-nearest neighbor用红色高亮显示
pcol <- as.character(as.numeric(data.test$Species))
pairs(data.test[1:4], pch = pcol, col = c("green3", "red")[(data.test$Species != fit)+1])
如上程序我们得到以下结果
四 常见问题
K值设定你需要掌握为多大?
k太小,分类结果易受噪声点影响;k太大,近邻中又可能包含太多的其它类别的点。(对距离加权,可以降低k值设定的影响)。k值通常是采用交叉检验来确定(以k=1为基准.经验规则:k一般低于训练样本数的平方根。类别如何判定最合适?
投票法没有考虑近邻的距离的远近,距离更近的近邻也许更应该决定最终的分类,所以加权投票法更恰当一些。如何选择合适的距离度量?
高维度对距离衡量的影响:众所周知当变量数越多,欧式距离的区分能力就越差。变量值域对距离的影响:值域越大的变量常常会在距离计算中占据主导作用,因此应先对变量进行标准化。训练样本是否要一视同仁?
在训练集中,有些样本可能是更值得依赖的。可以给不同的样本施加不同的权重,加强依赖样本的权重,降低不可信赖样本的影响。性能问题?
kNN是一种懒惰算法,平时不好好学习,考试(对测试样本分类)时才临阵磨枪(临时去找k个近邻)。懒惰的后果:构造模型很简单,但在对测试样本分类地的系统开销大,因为要扫描全部训练样本并计算距离。已经有一些方法提高计算的效率,例如压缩训练样本量等。