实验目的
了解回归分析算法的基本原理,并掌握R语言中实现回归算法的函数方法
实验原理
回归分析(regression analysis)指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。在大数据分析中,回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析以及发现变量之间的因果关系。例如,司机的鲁莽驾驶与道路交通事故数量之间的关系,最好的研究方法就是回归。
线性回归通常是人们在学习预测模型时首选的技术之一。在这种技术中,因变量是连续的,自变量可以是连续的也可以是离散的,回归线的性质是线性的。
线性回归可以根据给定的预测变量来预测目标变量的值。线性回归使用最佳的拟合直线(也就是回归线)在因变量(Y)和一个或多个自变量(X)之间建立一种关系。一元线性回归方程可以表示为下式:

实验步骤
我们使用R语言中的iris数据集进行回归分析,首先可以借助数据可视化来探索数据的规律和异常信息,可视化使数据看起来更简洁形象,比如在下面我们用散点图来观察数据集iris中各变量的关系。
加载iris数据集,调用str()函数查看iris数据集整体情况
> attach(iris)
> str(iris)
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
调用summary()函数总结iris数据集各变量的描述性统计量
> summary(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:50
Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
绘制散点矩阵图,查看数据集中各变量关系
> pairs(iris[, 1:4], col = "blue")
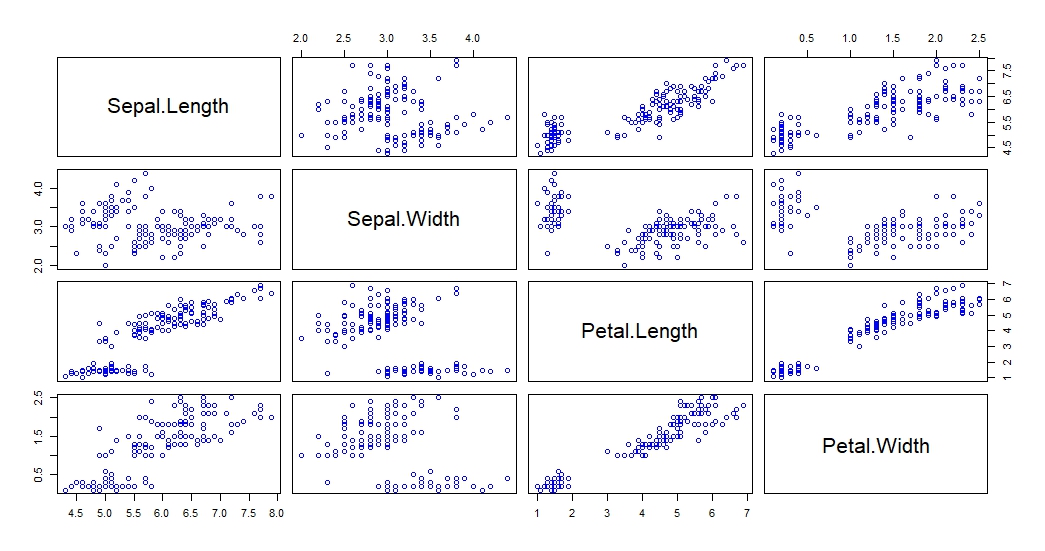
从上图可以看出,Petal.Length与Petal.Width存在明显的正相关性,接下来选择这组变量建立回归模型。
用lm()函数,得到回归方程
> (lm1 <- lm(Petal.Length ~ Petal.Width))
Call:
lm(formula = Petal.Length ~ Petal.Width)
Coefficients:
(Intercept) Petal.Width
1.084 2.230
由以上给出的系数可以得到拟合的回归方程为下式,其中y代表Petal.Length,x代表Petal.Width

查看回归结果
> summary(lm1)
Call:
lm(formula = Petal.Length ~ Petal.Width)
Residuals:
Min 1Q Median 3Q Max
-1.33542 -0.30347 -0.02955 0.25776 1.39453
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.08356 0.07297 14.85 <2e-16 ***
Petal.Width 2.22994 0.05140 43.39 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4782 on 148 degrees of freedom
Multiple R-squared: 0.9271, Adjusted R-squared: 0.9266
F-statistic: 1882 on 1 and 148 DF, p-value: < 2.2e-16
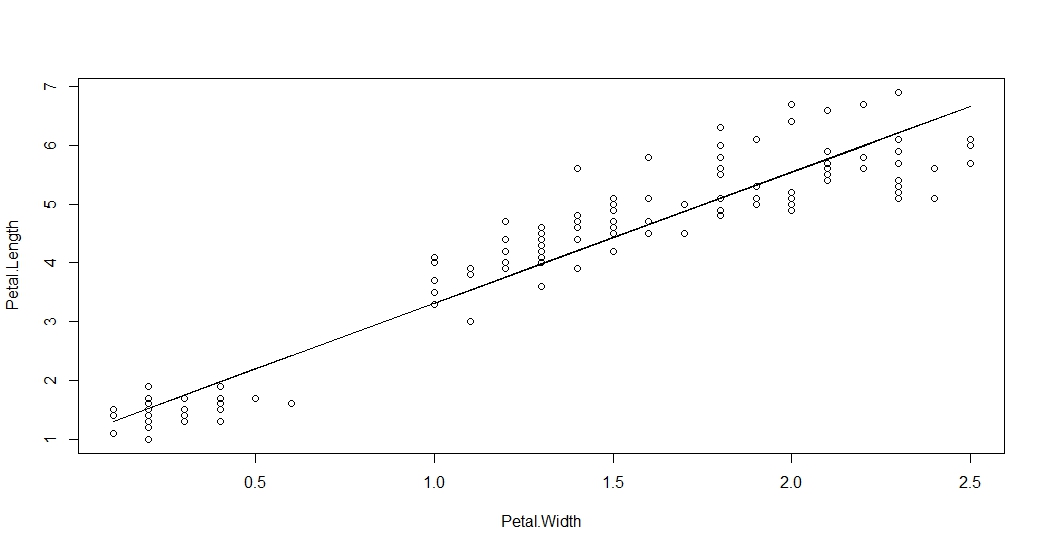
绘制Petal.Width和Petal.Length的散点图并添加回归线
> plot(Petal.Width, Petal.Length)
> lines(Petal.Width, lm1$fitted.values)
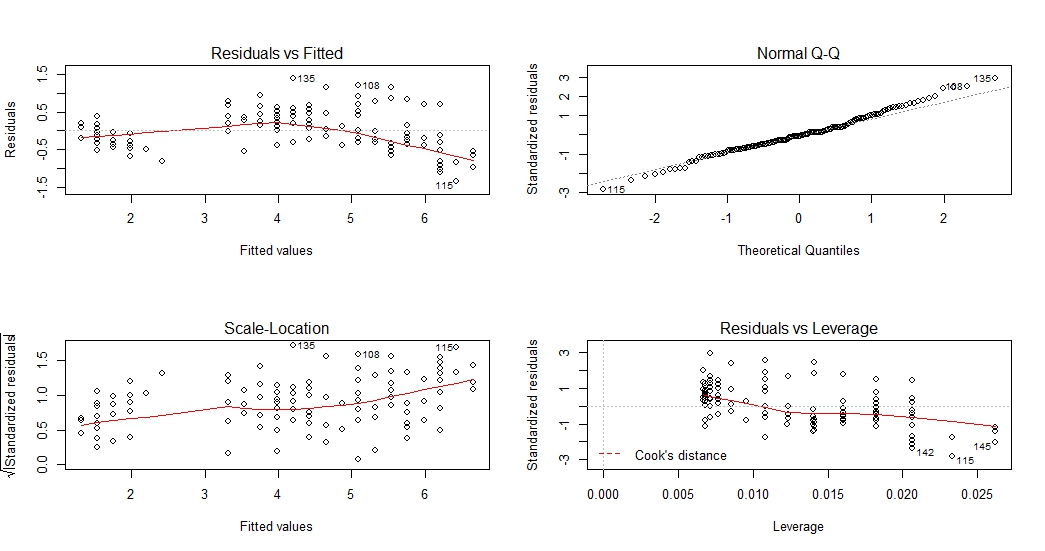
对拟合的模型进行残差检验
> par(mfrow = c(2, 2))
> plot(lm1)