泰坦尼克乘客生存预测
实验目的
熟悉使用R语言进行大数据综合分析的方法
实验原理
R工具是一套完整的的数据处理计算和制图软件系统。其功能包括:数据存储和处理系统;数组运算工具(其向量、矩阵运算方面功能尤其强大);完整连贯的统计分析工具;优秀的的统计制图功能;简便而强大的的编程语言:可操纵数据的输入和输出以及可实现分支、循环等用户自定义功能。
实验背景
泰坦尼克号的沉没是历史上最臭名昭著的沉船事件之一。1912年4月15日,泰坦尼克号在处女航中撞上冰山后沉没,造成2224名乘客和机组人员1502人遇难。这一耸人听闻的悲剧震惊了国际社会,并导致了对船舶安全的监管。
船只失事导致生命损失的原因之一是船上没有足够的救生艇供乘客和船员使用。尽管在沉船事件中幸存下来的一些因素,但有些人比其他人更容易生存,比如妇女、儿童和上层阶级。
在这个实验中,我们需要根据数据集中每个乘客的个人信息,以及他们是否幸存的结果。要求你完成对哪些人可能生存的分析。特别地,我们要求你应用机器学习的工具来预测哪些乘客在悲剧中幸存下来。
实验步骤
- 熟悉R环境;
- 打开R云件环境;
- 在相应编程环境中修改和运行代码;
- 查看结果。
实验一:数据读取
从Kaggle下载数据:titanic 加载包并读入数据,如提示包不存在可以用install.packages("包名")的方式安装
library('ggplot2') # 可视化
library('ggthemes') # 可视化
library('scales') # 可视化
library('dplyr') # 数据处理
library('mice') # 填充缺失数据
library('randomForest') # 分类算法
train <- read.csv('train.csv',stringsAsFactors= FALSE)
test <- read.csv('test.csv',stringsAsFactors= FALSE)
实验二:数据探索
合并两个数据框,查看相关变量名称
total_data <- bind_rows(train,test)
str(total_data)
查看的数据结果如下:
'data.frame': 1309 obs. of 12 variables:
$ PassengerId: int 1 2 3 4 5 6 7 8 9 10 ...
$ Survived : int 0 1 1 1 0 0 0 0 1 1 ...
$ Pclass : int 3 1 3 1 3 3 1 3 3 2 ...
$ Name : chr "Braund, Mr. Owen Harris" "Cumings, Mrs. John Bradley (Florence Briggs Thayer)" "Heikkinen" ...
$ Sex : chr "male" "female" "female" "female" ...
$ Age : num 22 38 26 35 35 NA 54 2 27 14 ...
$ SibSp : int 1 1 0 1 0 0 0 3 0 1 ...
$ Parch : int 0 0 0 0 0 0 0 1 2 0 ...
$ Ticket : chr "A/5 21171" "PC 17599" "STON/O2. 3101282" "113803" ...
$ Fare : num 7.25 71.28 7.92 53.1 8.05 ...
$ Cabin : chr "" "C85" "" "C123" ...
$ Embarked : chr "S" "C" "S" "S" ...
我们观察到一共有1309条数据,每一条数据有12个相关变量
$ PassengerId: 乘客编号
$ Survived :存活情况(存活:1 ; 死亡:0)
$ Pclass : 客场等级
$ Name : 乘客姓名
$ Sex : 性别
$ Age : 年龄
$ SibSp : 同乘的兄弟姐妹/配偶数
$ Parch : 同乘的父母/小孩数
$ Ticket : 船票编号
$ Fare : 船票价格
$ Cabin :客舱号
$ Embarked : 登船港口
实验三:数据预处理
1.变量划分
乘客名称
注意到在乘客名字(Name)中,有一个非常显著的特点:乘客头衔每个名字当中都包含了具体的称谓或者说是头衔,将这部分信息提取出来后可以作为非常有用一个新变量,可以帮助我们进行预测。此外也可以用乘客的姓代替家庭,生成家庭变量。
# 从名称中挖掘
# 从乘客名字中提取头衔
#R中的grep、grepl、sub、gsub、regexpr、gregexpr等函数都使用正则表达式的规则进行匹配。默认是egrep的规则,sub函数只实现第一个位置的替换,gsub函数实现全局的替换。
total_data$Title <- gsub('(.*, )|(\\..*)', '', total_data$Name)
# 查看按照性别划分的头衔数量
table(total_data$Sex, total_data$Title)
结果如下:
Capt Col Don Dona Dr Jonkheer Lady Major Master Miss Mlle Mme Mr Mrs Ms Rev Sir the Countess
female 0 0 0 1 1 0 1 0 0 260 2 1 0 197 2 0 0 1
male 1 4 1 0 7 1 0 2 61 0 0 0 757 0 0 8 1 0
我们发现头衔的类别太多,并且好多出现的频次是很低的,我们可以将这些类别进行合并
# 合并低频头衔为一类
rare_title <- c('Dona', 'Lady', 'the Countess','Capt', 'Col', 'Don',
'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer')
# 重命名称呼
total_data$Title[total_data$Title == 'Mlle'] <- 'Miss'
total_data$Title[total_data$Title == 'Ms'] <- 'Miss'
total_data$Title[total_data$Title == 'Mme'] <- 'Mrs'
total_data$Title[total_data$Title %in% rare_title] <- 'Rare Title'
# 再次查看按照性别划分的头衔数量
table(total_data$Sex, total_data$Title)
得到如下结果:
Master Miss Mr Mrs Rare Title
female 0 264 0 198 4
male 61 0 757 0 25
最后,从名称中获取到姓氏
#sapply()函数:根据传入参数规则重新构建一个合理的数据类型返回
total_data$Surname <- sapply(total_data$Name, function(x) strsplit(x, split = '[,.]')[[1]][1])
家庭成员数量
既然我们已经根据乘客的名字划分成一些新的变量,我们可以把它进一步做一些新的家庭变量。首先我们要做一个基于兄弟姐妹/配偶数量和儿童/父母数量的家庭规模变量。
# 创建一个包含乘客自己的家庭规模变量
total_data$Fsize <- total_data$SibSp + total_data$Parch + 1
# Create a family variable
total_data$Family <- paste(total_data$Surname, total_data$Fsize, sep='_')
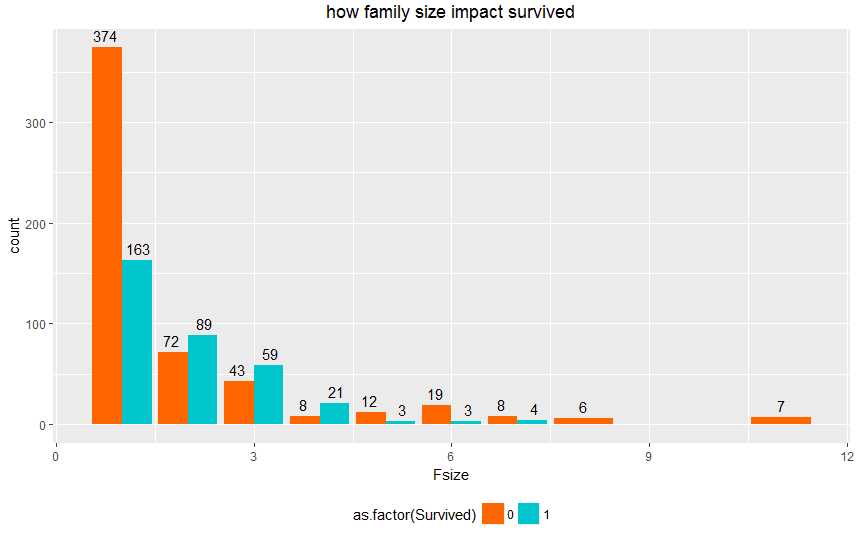
# 为了直观显示,我们可以用ggplot2 画出家庭成员数量和生存家庭数情况的图形
ggplot(total_data[!is.na(total_data$Survived),],aes(x= Fsize,fill = as.factor(Survived)))+
geom_bar(stat = 'count',position = 'dodge')+
ggtitle('how family size impact survived')+
scale_fill_manual(values=c("#FF6600", "#00C5CD")) +
geom_text(stat = "count", aes(label = ..count..), position=position_dodge(width=1), vjust=-0.5) +
theme(plot.title = element_text(hjust = 0.5), legend.position="bottom")
结果如下:
2.缺失值填补
观察文件中的数据,我们会发现有些乘客的信息参数并不完整,由于所给的数据集并不大,我们不能通过删除一行或者一列来处理缺失值,因而对于我们关注的一些字段参数,我们需要根据统计学的描述数据(平均值、中位数等等)来合理给出缺失值。 我们可以通过函数查看缺失数据的变量在第几条数据出现缺失和总共缺失的个数
年龄的缺失和填补
#统计年龄的缺失个数
age_null_count <- sum(is.na(total_data$Age))
#age_null_count = 263
通常我们会使用 rpart (recursive partitioning for regression) 包来做缺失值预测 在这里我将使用 mice 包进行处理。我们先要对因子变量(factor variables)因子化,然后再进行多重插补法。
#统计年龄的缺失处理
age_null_count <- sum(is.na(total_data$Age))
# 使自变量因子化
factor_vars <- c('PassengerId','Pclass','Sex','Embarked',
'Title','Surname','Family','Fsize')
#lapply()返回一个长度与X一致的列表,每个元素为FUN计算出的结果,且分别对应到X中的每个元素。
total_data[factor_vars] <- lapply(total_data[factor_vars],function(x) as.factor(x))
# 设置随机值
set.seed(129)
# 执行多重插补法,剔除一些没什么用的变量:
mice_mod <- mice(total_data[, !names(total_data) %in% c('PassengerId','Name','Ticket','Cabin','Family','Surname','Survived')], method='rf')
# 保存完成的输出
mice_output <- complete(mice_mod)
让我们来比较一下我们得到的结果与原来的乘客的年龄分布以确保没有明显的偏差
# 绘制直方图
par(mfrow=c(1,2))
hist(total_data$Age, freq=F, main='Age: Original Data',
col='darkgreen', ylim=c(0,0.04))
hist(mice_output$Age, freq=F, main='Age: MICE Output',
col='lightgreen', ylim=c(0,0.04))
结果如下,右边图和左边图有很高的相似度
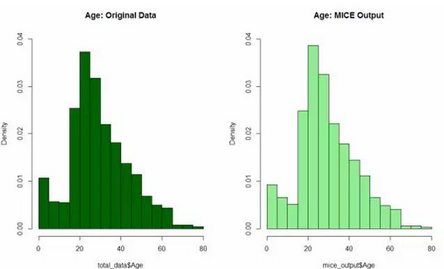
所以,我们可以用mice模型的结果对原年龄数据进行替换。
# 用mice模型数据替换原始数据
total_data$Age <- mice_output$Age
# 再次查看年龄的缺失值数据
sum(is.na(total_data$Age))
# 0
票价的缺失处理
#查看票价的缺失值
getFareNullID <- function(total_data){
count <- 0
for(i in 1:nrow(total_data))
if(is.na(total_data$Fare[i])){
#打印缺失票价的具体行数
print(i);
count <- count + 1
}
return(count)
}
fare_null_count <- getFareNullID(total_data)
#fare_null_count = 1
得到票价缺失个数为1 ,缺失行数为第1044行。查看这一行我们会发现
total_data[1044,]
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin
1044 1044 NA 3 Storey, Mr. Thomas male 60.5 0 0 3701 NA
Embarked Title Surname Fsize Family
1044 S Mr Storey 1 Storey_1
我们发现港口和舱位是完整的,我们可以根据相同的港口和相同的舱位来大致估计该乘客的票价,我们取这些类似乘客的中位数来替换缺失的值
#从港口Southampton ('S')出发的三等舱乘客。 从相同港口出发且处于相同舱位的乘客数目
same_farenull <- sum(total_data$Pclass == '3' & total_data$Embarked == 'S')
# 基于出发港口和客舱等级,替换票价缺失值
total_data$Fare[1044] <- median(total_data[total_data$Pclass == '3' & total_data$Embarked == 'S', ]$Fare, na.rm = TRUE)
登船港口号的缺失处理
#登船港口号的缺失值函数
getEmbarkedNullCount <- function(total_data) {
count0 <- 0
count <- 0
for(i in 1:nrow(total_data))
if(total_data$Embarked[i] == ""){
#可以打印出缺失的所在行数
print(i);
count <- count + 1
}
return(count)
}
#登船港口号的缺失个数
embarked_null_count <- getEmbarkedNullCount(total_data)
#embarked_null_count 2
得到登船港口号缺失的个数为2 ,分别为 62 、830,我估计对于有相同舱位等级(passenger class)和票价(Fare)的乘客也许有着相同的 登船港口位置embarkment .我们可以看到他们支付的票价分别为: $ 80 和 $ 80 同时他们的舱位等级分别是: 1 和 1 . 我们可以用箱线图绘制出这三者之间关系图
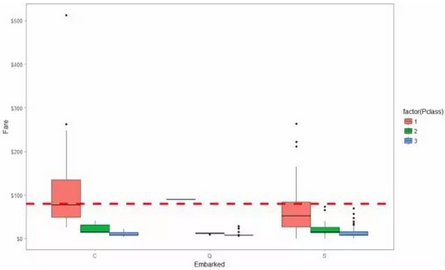
从港口 (‘C’)出发的头等舱支付的票价的中位数正好为80。因此我们可以放心的把处于头等舱且票价在$80的乘客62和830 的出发港口缺失值替换为’C’
total_data$Embarked[c(62, 830)] <- 'C'
实验四:分析建模
年龄的划分
我们考虑将年龄划分成三个阶段,小于18岁算小孩,18岁及以上至50岁为青壮年,50岁以上为老年人
#将年龄划分成3个阶段
total_data$AgeGroup[total_data$Age < 18] <- 'child'
total_data$AgeGroup[total_data$Age >= 18 & total_data$Age <= 50] <- 'young'
total_data$AgeGroup[total_data$Age > 50] <- 'old'
table(total_data$AgeGroup,total_data$Survived)
#得到如下结果
0 1
child 69 66
old 51 28
young 429 248
相比于成人,小孩的生存概率接近50%,小孩得到的照顾比成年高的多
是否为母亲
我们从性别和头衔中提炼出一位成年女性是否为一位母亲,看看她的生存概率如何
# Adding Mother variable
total_data$IsMother <- 'Not'
total_data$IsMother[total_data$Sex == 'female' & total_data$Parch > 0 & total_data$Age > 18 & total_data$Title != 'Miss'] <- 'Yes'
# Show counts
table(total_data$IsMother, total_data$Survived)
#结果如下:
0 1
Not 533 303
Yes 16 39
我们发现,如果是一位母亲,那么你生存下来的概率高达70%,之后,我们整合上面两个新变量到原数据集
# 完成因子化
total_data$AgeGroup <- factor(total_data$AgeGroup)
total_data$IsMother <- factor(total_data$IsMother)
#mice 包中显示缺失数据的一种模式。
md.pattern(total_data)
预测
拆分测试和训练数据集
#拆分数据集
train <- total_data[1:891,]
test <- total_data[892:1309,]
构建训练模型
我们使用随机森林法则作用于训练数据集来构建我们需要的预测模型
#拆分数据集
train <- total_data[1:891,]
test <- total_data[892:1309,]
set.seed(754)
# 构建预测模型
rf_model <- randomForest(factor(Survived) ~ Pclass + Sex + Age + SibSp + Parch
+ Fare + Embarked + Title
+ Fsize + AgeGroup + IsMother,
data = train)
实验五:模型评价与优化
# 展示模型预测的错误率
# OOB:在构造单棵决策树时我们只是随机有放回的抽取了N个样例,用没有抽取到的样例来测试
plot(rf_model, ylim=c(0,0.36))
mlabels <- factor(rf_model,levels = c(1,2,3),labels = c("OOB","0","1"))
legend('topright', colnames(rf_model$err.rate),levels(mlabels) ,col=1:3, fill=1:3)
结果如下
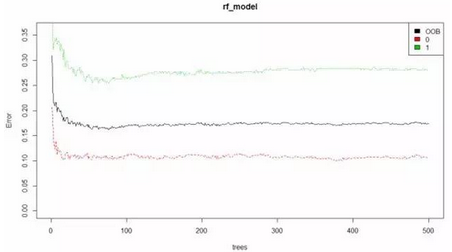
黑色那条线表示:整体误差率(the overall error rate)低于20% 红色和绿色分别表示:遇难与生还的误差率 至此相对于生还来说,我们可以更准确的预测出死亡。
实验六:可视化输出
相关性检测
通过随机森林中所有决策树的Gini 计算出其他变量相对于生存变量的相关性排行,我们可以看出那些因素对生存率影响较大
# 重要性系数
importance <- importance(rf_model)
varImportance <- data.frame(Variables = row.names(importance),
Importance = round(importance[ ,'MeanDecreaseGini'],2))
# 创建基于重要性系数排列的变量
rankImportance <- varImportance %>%
mutate(Rank = paste0('#',dense_rank(desc(Importance))))
# 使用 ggplot2 绘出重要系数的排名
ggplot(rankImportance, aes(x = reorder(Variables, Importance),
y = Importance, total_data = Importance)) +
geom_bar(stat='identity') +
geom_text(aes(x = Variables, y = 0.5, label = Rank),
hjust=0, vjust=0.55, size = 4, colour = 'red') +
labs(x = 'Variables') +
coord_flip() +
theme_bw()
结果如下:
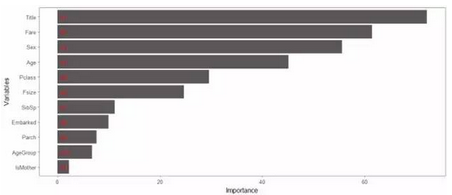
我们发现,头衔称号和船票价格及性别年龄对生存率的影响比较大,我们刚刚认为的小孩、老人和是否为母亲 这几个特征应该有很大的生存几率,但是结果并不是这样,现实还是比较残酷。