实验目的
掌握Python语言对数据集数据特征的分析方法
实验原理
对数据进行质量分析后,接下来可以通过绘制图表、计算统计量等手段对数据进行特征分析。
特征分析主要有分布分析、统计量分析、周期性分析、相关性分析等等
实验步骤
注意:python2中print语句不加括号,python3中print语句打印内容要加括号!
频数分析
1 定性分析(柱状图、饼形图)
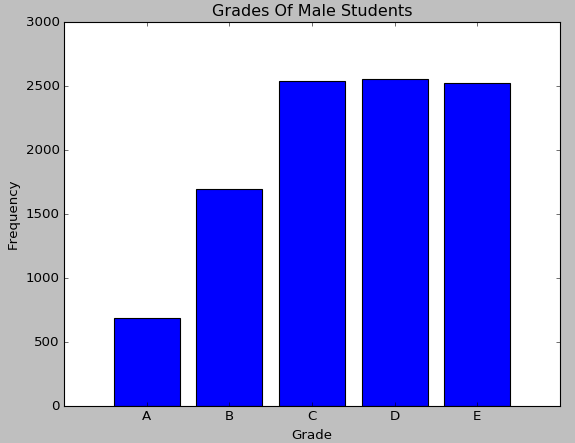
柱状图是以柱的高度来指代某种类型的频数,使用Matplotlib对成绩这一定性变量绘制柱状图的代码如下:
1 from matplotlib import pyplot
2
3 #绘制柱状图
4 def drawBar(grades):
5 xticks = ['A', 'B', 'C', 'D', 'E']
6 gradeGroup = {}
7 #对每一类成绩进行频数统计
8 for grade in grades:
9 gradeGroup[grade] = gradeGroup.get(grade, 0) + 1
10 #创建柱状图
11 #第一个参数为柱的横坐标
12 #第二个参数为柱的高度
13 #参数align为柱的对齐方式,以第一个参数为参考标准
14 pyplot.bar(range(5), [gradeGroup.get(xtick, 0) for xtick in xticks], align='center')
15
16 #设置柱的文字说明
17 #第一个参数为文字说明的横坐标
18 #第二个参数为文字说明的内容
19 pyplot.xticks(range(5), xticks)
20
21 #设置横坐标的文字说明
22 pyplot.xlabel('Grade')
23 #设置纵坐标的文字说明
24 pyplot.ylabel('Frequency')
25 #设置标题
26 pyplot.title('Grades Of Male Students')
27 #绘图
28 pyplot.show()
29
30 drawBar(grades)
绘制出来的柱状图的效果如下:
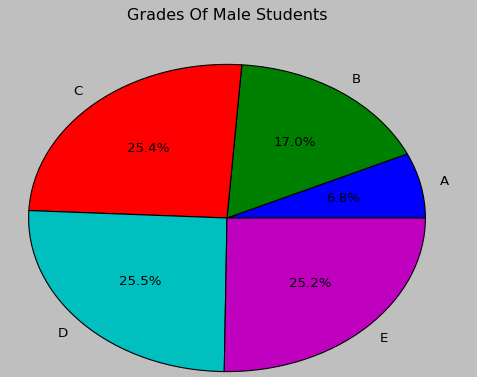
而饼形图是以扇形的面积来指代某种类型的频率,使用Matplotlib对成绩这一定性变量绘制饼形图的代码如下:
1 from matplotlib import pyplot
2
3 #绘制饼形图
4 def drawPie(grades):
5 labels = ['A', 'B', 'C', 'D', 'E']
6 gradeGroup = {}
7 for grade in grades:
8 gradeGroup[grade] = gradeGroup.get(grade, 0) + 1
9 #创建饼形图
10 #第一个参数为扇形的面积
11 #labels参数为扇形的说明文字
12 #autopct参数为扇形占比的显示格式
13 pyplot.pie([gradeGroup.get(label, 0) for label in labels], labels=labels, autopct='%1.1f%%')
14 pyplot.title('Grades Of Male Students')
15 pyplot.show()
16
17 drawPie(grades)
绘制出来的饼形图效果如下:
2 定量分析(直方图、累积曲线)
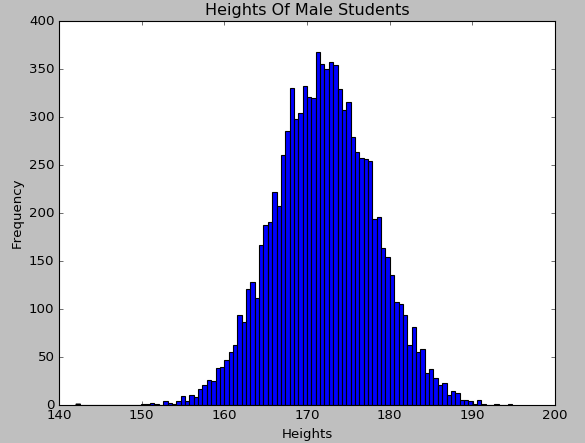
直方图类似于柱状图,是用柱的高度来指代频数,不同的是其将定量数据划分为若干连续的区间,在这些连续的区间上绘制柱。使用Matplotlib对身高这一定量变量绘制直方图的代码如下:
1 from matplotlib import pyplot
2
3 #绘制直方图
4 def drawHist(heights):
5 #创建直方图
6 #第一个参数为待绘制的定量数据,不同于定性数据,这里并没有事先进行频数统计
7 #第二个参数为划分的区间个数
8 pyplot.hist(heights, 100)
9 pyplot.xlabel('Heights')
10 pyplot.ylabel('Frequency')
11 pyplot.title('Heights Of Male Students')
12 pyplot.show()
13
14 drawHist(heights)
直方图对应数据的密度函数,由于身高变量是属于服从正态分布的,从绘制出来的直方图上也可以直观地看出来:
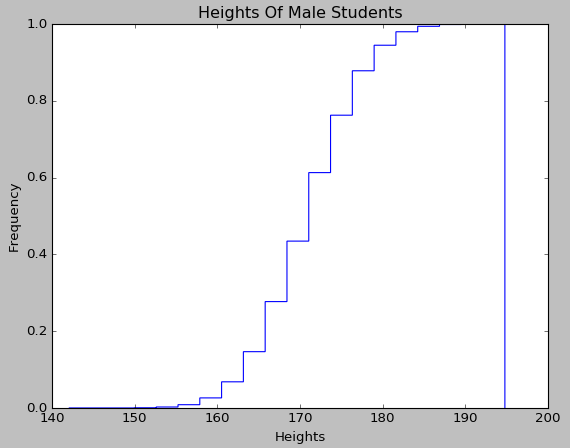
使用Matplotlib对身高这一定量变量绘制累积曲线的代码如下:
1 from matplotlib import pyplot
2
3 #绘制累积曲线
4 def drawCumulativeHist(heights):
5 #创建累积曲线
6 #第一个参数为待绘制的定量数据
7 #第二个参数为划分的区间个数
8 #normed参数为是否无量纲化
9 #histtype参数为'step',绘制阶梯状的曲线
10 #cumulative参数为是否累积
11 pyplot.hist(heights, 20, normed=True, histtype='step', cumulative=True)
12 pyplot.xlabel('Heights')
13 pyplot.ylabel('Frequency')
14 pyplot.title('Heights Of Male Students')
15 pyplot.show()
16
17 drawCumulativeHist(heights)
累积曲线对应数据的分布函数,由于身高变量是属于服从正态分布的,从绘制出来的累积曲线图上也可以直观地看出来:
3 关系分析(散点图)
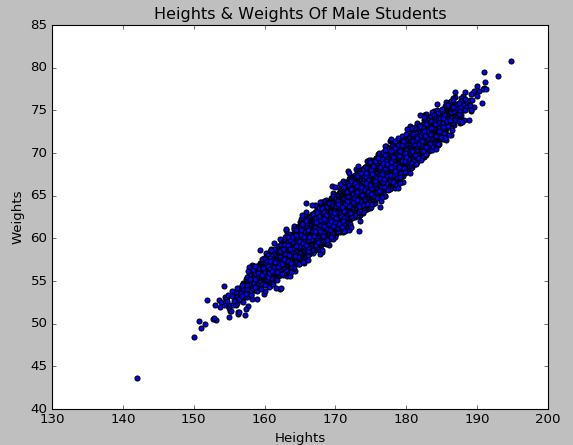
在散点图中,分别以自变量和因变量作为横纵坐标。当自变量与因变量线性相关时,在散点图中,点近似分布在一条直线上。我们以身高作为自变量,体重作为因变量,讨论身高对体重的影响。使用Matplotlib绘制散点图的代码如下:
- ` from matplotlib import pyplot `
- `#绘制散点图 `
- `def drawScatter(heights, weights): `
- ` #创建散点图 `
- ` #第一个参数为点的横坐标 `
- ` #第二个参数为点的纵坐标 `
- ` pyplot.scatter(heights, weights) `
- ` pyplot.xlabel('Heights') `
- ` pyplot.ylabel('Weights') `
- ` pyplot.title('Heights & Weights Of Male Students') `
- ` pyplot.show() `
- ` drawScatter(heights, weights) `
我们在创建数据时,体重这一变量的确是由身高变量通过线性回归产生,绘制出来的散点图如下:
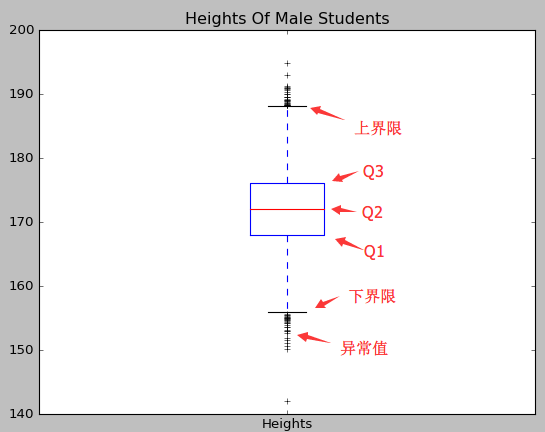
4 探索分析(箱形图)
在不明确数据分析的目标时,我们对数据进行一些探索性的分析,通过我们可以知道数据的中心位置,发散程度以及偏差程度。使用Matplotlib绘制关于身高的箱形图的代码如下:
1 from matplotlib import pyplot
2
3 #绘制箱形图
4 def drawBox(heights):
5 #创建箱形图
6 #第一个参数为待绘制的定量数据
7 #第二个参数为数据的文字说明
8 pyplot.boxplot([heights], labels=['Heights'])
9 pyplot.title('Heights Of Male Students')
10 pyplot.show()
11
12 drawBox(heights)
绘制出来的箱形图中,包含3种信息:
- Q2所指的红线为中位数
- Q1所指的蓝框下侧为下四分位数,Q3所指的蓝框上侧为上四分位数,Q3-Q1为四分为差。四分位差也是衡量数据的发散程度的指标之一。
- 上界线和下界线是距离中位数1.5倍四分位差的线,高于上界线或者低于下界线的数据为异常值。