作业22答案
练习1 神经网络分类训练
- 解释说明感知机的原理
- 解释通过感知机如何组合成神经网络
- 使用Python实现神经网络算法
print(__doc__)
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import MinMaxScaler
from sklearn import datasets
# different learning rate schedules and momentum parameters
params = [{'solver': 'sgd', 'learning_rate': 'constant', 'momentum': 0,
'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'constant', 'momentum': .9,
'nesterovs_momentum': False, 'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'constant', 'momentum': .9,
'nesterovs_momentum': True, 'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': 0,
'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': .9,
'nesterovs_momentum': True, 'learning_rate_init': 0.2},
{'solver': 'sgd', 'learning_rate': 'invscaling', 'momentum': .9,
'nesterovs_momentum': False, 'learning_rate_init': 0.2},
{'solver': 'adam', 'learning_rate_init': 0.01}]
labels = ["constant learning-rate", "constant with momentum",
"constant with Nesterov's momentum",
"inv-scaling learning-rate", "inv-scaling with momentum",
"inv-scaling with Nesterov's momentum", "adam"]
plot_args = [{'c': 'red', 'linestyle': '-'},
{'c': 'green', 'linestyle': '-'},
{'c': 'blue', 'linestyle': '-'},
{'c': 'red', 'linestyle': '--'},
{'c': 'green', 'linestyle': '--'},
{'c': 'blue', 'linestyle': '--'},
{'c': 'black', 'linestyle': '-'}]
def plot_on_dataset(X, y, ax, name):
# for each dataset, plot learning for each learning strategy
print("\nlearning on dataset %s" % name)
ax.set_title(name)
X = MinMaxScaler().fit_transform(X)
mlps = []
if name == "digits":
# digits is larger but converges fairly quickly
max_iter = 15
else:
max_iter = 400
for label, param in zip(labels, params):
print("training: %s" % label)
mlp = MLPClassifier(verbose=0, random_state=0,
max_iter=max_iter, **param)
mlp.fit(X, y)
mlps.append(mlp)
print("Training set score: %f" % mlp.score(X, y))
print("Training set loss: %f" % mlp.loss_)
for mlp, label, args in zip(mlps, labels, plot_args):
ax.plot(mlp.loss_curve_, label=label, **args)
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# load / generate some toy datasets
iris = datasets.load_iris()
digits = datasets.load_digits()
data_sets = [(iris.data, iris.target),
(digits.data, digits.target),
datasets.make_circles(noise=0.2, factor=0.5, random_state=1),
datasets.make_moons(noise=0.3, random_state=0)]
for ax, data, name in zip(axes.ravel(), data_sets, ['iris', 'digits',
'circles', 'moons']):
plot_on_dataset(*data, ax=ax, name=name)
fig.legend(ax.get_lines(), labels=labels, ncol=3, loc="upper center")
plt.show()
练习2 分类算法训练
- 了解其他分类算法的原理和实现方法
- 解释朴素贝叶斯算法的分类原理,并在Python上实现贝叶斯分类
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
iris=datasets.load_iris()
clf=GaussianNB()
clf.fit(iris.data,tris.target)
clf.predict(iris.data[0].reshape(1,-1))
练习3 分类算法比较
- 解释各种分类算法的优缺点以及适用场景
- 在网上搜索分类数据集进行分类实验,比较多种分类算法的优劣
练习4 模型集成训练
- 了解GBDT,并和随机森林算法进行比较,了解模型集成思想
练习5 其他训练
完成反向传播算法的推导过程
反向传播算法(Backpropagation)是目前用来训练人工神经网络(Artificial Neural Network,ANN)的最常用且最有效的算法。其主要思想是:(1)将训练集数据输入到ANN的输入层,经过隐藏层,最后达到输出层并输出结果,这是ANN的前向传播过程; (2)由于ANN的输出结果与实际结果有误差,则计算估计值与实际值之间的误差,并将该误差从输出层向隐藏层反向传播,直至传播到输入层; (3)在反向传播的过程中,根据误差调整各种参数的值;不断迭代上述过程,直至收敛。
采用BP算法从输出层、经过隐层再到输入层进行层层计算的原因是如果直接计算误差函数相对于各权值的偏导很难得到显式的表达函数(最小均方算法或Widrow-Hoff学习算法),采用从后向前递推的方式大幅度的利用了前期的计算值,也使得网络具备了更多的灵活性。使用均方误差作为性能指数,那么优化算法的目标就是调整网络的参数使得均方误差最小化。那么根据最速下降算法的原理,第k次迭代计算得到的权值和偏移如下:

其中,m是层序号,i是神经元在层中序号,j则是一个神经元的输入的序号,是均方误差。
前面就提到了,求这两个偏导是很困难的事情,因此可以使用链式法则从最后一层向前计算。根据链式法则,可以将偏导分解如下:
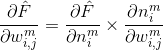
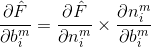
采用矩阵的表示方法来表示神经元的计算,如下面这个图所示。
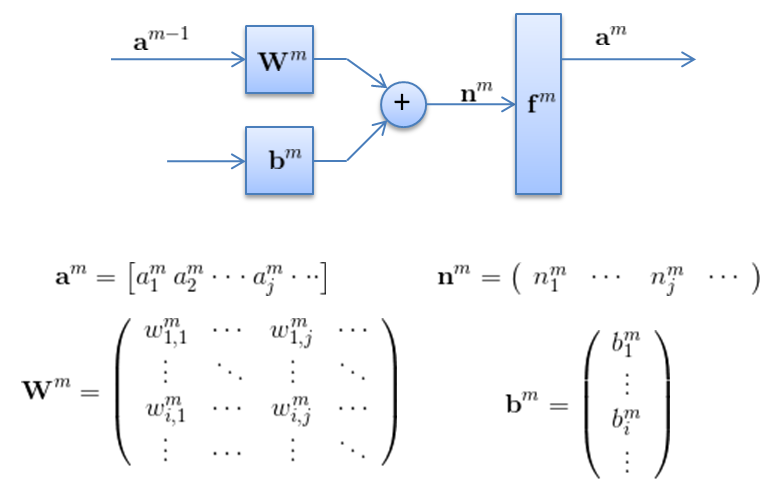
经过一系列推导可以得到:
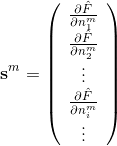
的表达式。
对于BP算法来说,最后一层的计算(第M层)是所有计算的开始。其矩阵形式的表达式为:
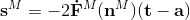
这里面存在一个系数2,是因为使用的是均方误差,平方求导会有系数2.
因此如果用矩阵形式表示,那么权值和偏置值更新的表达式是: