实验目的

了解基本k邻近算法的基本原理，并掌握Python语言中实现聚类算法的函数方法

实验原理

聚类就是将相似的事物聚集在一起，而将不相似的事物划分到不同的类别的过程，是数据分析之中十分重要的一种手段。在数据分析的术语之中，聚类和分类是两种技术。分类是指我们已经知道了事物的类别，需要从样品中学习分类的规则，是一种监督式学习；而聚类则是由我们来给定简单的规则，从而得到类别，是一种无监督学习。

在K均值算法中，质心是定义聚类原型（也就是机器学习获得的结果）的核心。在介绍算法实施的具体过程中，我们将演示质心的计算方法。而且你将看到除了第一次的质心是被指定的以外，此后的质心都是经由计算均值而获得的。

首先，选择K个初始质心（这K个质心并不要求来自于样本数据集），其中K是用户指定的参数，也就是所期望的簇的个数。每个数据点都被收归到距其最近之质心的分类中，而同一个质心所收归的点集为一个簇。然后，根据本次分类的结果，更新每个簇的质心。重复上述数据点分类与质心变更步骤，直到簇内数据点不再改变，或者等价地说，直到质心不再改变。

实验步骤

一、kNN算法分析

K最近邻（k-Nearest Neighbor，KNN）分类算法可以说是最简单的机器学习算法了。它采用测量不同特征值之间的距离方法进行分类。它的思想很简单：如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。

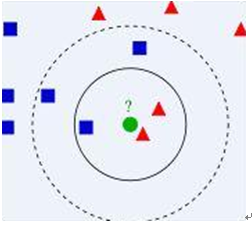
比如上面这个图，我们有两类数据，分别是蓝色方块和红色三角形，他们分布在一个上图的二维中间中。那么假如我们有一个绿色圆圈这个数据，需要判断这个数据是属于蓝色方块这一类，还是与红色三角形同类。怎么做呢？我们先把离这个绿色圆圈最近的几个点找到，因为我们觉得离绿色圆圈最近的才对它的类别有判断的帮助。那到底要用多少个来判断呢？这个个数就是k了。如果k=3，就表示我们选择离绿色圆圈最近的3个点来判断，由于红色三角形所占比例为2/3，所以我们认为绿色圆是和红色三角形同类。如果k=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。从这里可以看到，k的值还是很重要的。

KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。因此可以采用权值的方法（和该样本距离小的邻居权值大）来改进。该方法的另一个不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

总的来说就是我们已经存在了一个带标签的数据库，然后输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似（最近邻）的分类标签。一般来说，只选择样本数据库中前k个最相似的数据。最后，选择k个最相似数据中出现次数最多的分类。其算法描述如下：

1）计算已知类别数据集中的点与当前点之间的距离；

2）按照距离递增次序排序；

3）选取与当前点距离最小的k个点；

4）确定前k个点所在类别的出现频率；

5）返回前k个点出现频率最高的类别作为当前点的预测分类。

二、Python实现

对于机器学习而已，Python需要额外安装三件宝，分别是Numpy，scipy和Matplotlib。前两者用于数值计算，后者用于画图。安装很简单，直接到各自的官网下载回来安装即可。安装程序会自动搜索我们的python版本和目录，然后安装到python支持的搜索路径下。反正就python和这三个插件都默认安装就没问题了。

另外，如果我们需要添加我们的脚本目录进Python的目录（这样Python的命令行就可以直接import），可以在系统环境变量中添加：PYTHONPATH环境变量，值为我们的路径，例如：E:\Python\Machine Learning in Action

一般实现一个算法后，我们需要先用一个很小的数据库来测试它的正确性，否则一下子给个大数据给它，它也很难消化，而且还不利于我们分析代码的有效性。

首先，我们新建一个kNN.py脚本文件，文件里面包含两个函数，一个用来生成小数据库，一个实现kNN分类算法。代码如下：

# -*- coding: utf-8 -*-

###实现在坐标系中把数据点展现出来

from numpy import *

import numpy as np

import matplotlib.pyplot as plt

###产生训练数据集，共4个点

def createDataSet():

group = array\(\[\[1.0,1.1\],\[1.0,1.0\],\[0,0\],\[0,0.1\]\]\)

labels = \['A','A','B','B'\] \#这4个点所对应的类别，即贴上标签

return group,labels

##testdata = [0.2,0.2] #测试数据集，一个点

###绘制图形

dataSet,labels = createDataSet()

fig = plt.figure()

ax = fig.add_subplot(111)

indx = 0

for point in dataSet:

if labels\[indx\] == 'A':

    ax.scatter\(point\[0\],point\[1\],c = 'blue',marker = 'o',linewidths=0,s=300\)

    plt.annotate\("\("+str\(point\[0\]\)+","+str\(point\[1\]\)+"\)",xy = \(point\[0\],point\[1\]\)\)

else:

    ax.scatter\(point\[0\],point\[1\],c = 'red',marker = '^',linewidths=0,s=300\)

    plt.annotate\("\("+str\(point\[0\]\)+","+str\(point\[1\]\)+"\)",xy = \(point\[0\],point\[1\]\)\)

indx +=1

###将测试数据集（需要分类的那个点）也绘制出来

#ax.scatter(testdata[0],testdata[1],c = 'green',marker = '^',linewidths=0,s=300)

#plt.annotate("("+str(testdata[0])+","+str(testdata[1])+")",xy = (testdata[0],testdata[1]))

plt.show()