神经网络分类算法

一 实验目的

  1. 了解感知机的原理
  2. 了解通过感知机如何组合成神经网络
  3. 学会使用R或者Pyhton工具建立神经网络模型用于分类

二 实验原理

人工神经网络（ANN），简称神经网络，是一种模仿生物神经网络的结构和功能的数学模型或计算模型。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统。现代神经网络是一种非线性统计性数据建模工具，常用来对输入和输出间复杂的关系进行建模，或用来探索数据的模式。

人工神经网络从以下四个方面去模拟人的智能行为:

  • 物理结构：人工神经元将模拟生物神经元的功能
  • 计算模拟：人脑的神经元有局部计算和存储的功能，通过连接构成一个系统。人工神经网络中也有大量有局部处理能力的神经元，也能够将信息进行大规模并行处理
  • 存储与操作：人脑和人工神经网络都是通过神经元的连接强度来实现记忆存储功能，同时为概括、类比、推广提供有力的支持

  • 训练：同人脑一样，人工神经网络将根据自己的结构特性，使用不同的训练、学习过程，自动从实践中获得相关知识

    神经网络是一种运算模型，由大量的节点（或称“神经元”，或“单元”）和之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。

感知器

历史上，科学家一直希望模拟人的大脑，造出可以思考的机器。人为什么能够思考？科学家发现，原因在于人体的神经网络。

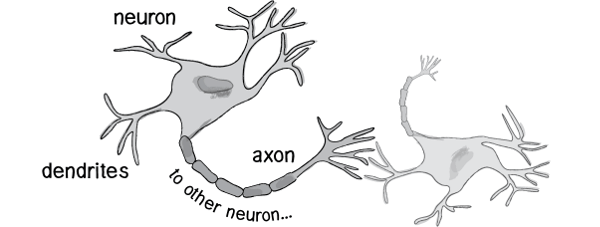
  1. 外部刺激通过神经末梢，转化为电信号，转导到神经细胞（又叫神经元）。
  2. 无数神经元构成神经中枢。
  3. 神经中枢综合各种信号，做出判断
  4. 人体根据神经中枢的指令，对外部刺激做出反应。

既然思考的基础是神经元，如果能够"人造神经元"（artificial neuron），就能组成人工神经网络，模拟思考。上个世纪六十年代，提出了最早的"人造神经元"模型，叫做"感知器"（perceptron），直到今天还在用。

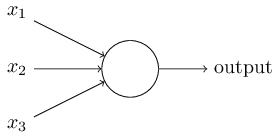
上图的圆圈就代表一个感知器。它接受多个输入（x1，x2，x3...），产生一个输出（output），好比神经末梢感受各种外部环境的变化，最后产生电信号。

为了简化模型，我们约定每种输入只有两种可能：1 或 0。如果所有输入都是1，表示各种条件都成立，输出就是1；如果所有输入都是0，表示条件都不成立，输出就是0

决策模型

单个的感知器构成了一个简单的决策模型，已经可以拿来用了。真实世界中，实际的决策模型则要复杂得多，是由多个感知器组成的多层网络。

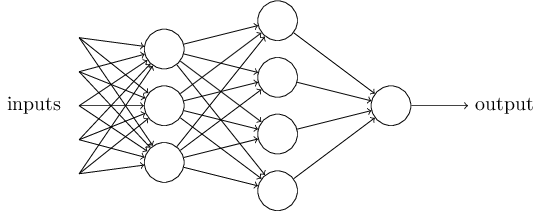
上图中，底层感知器接收外部输入，做出判断以后，再发出信号，作为上层感知器的输入，直至得到最后的结果。（注意：感知器的输出依然只有一个，但是可以发送给多个目标。）

一个神经网络的搭建，需要满足三个条件。

  • 输入和输出

  • 权重（W）和阈值（b）

  • 多层感知机的结构

神经网络的运作过程如下：

确定输入和输出

  1. 找到一种或多种算法，可以从输入得到输出
  2. 找到一组已知答案的数据集，用来训练模型，估算W和b
  3. 一旦新的数据产生，输入模型，就可以得到结果，同时对W和b进行校正

可以看到，整个过程需要海量计算。所以，神经网络直到最近这几年才有实用价值，而且一般的 CPU 还不行，要使用专门为机器学习定制的 GPU 来计算。

三 实验步骤

我们以鸢尾花数据集为例，由于单层感知器是一个二分类器，所以我们将鸢尾花数据也分为两类，“setosa”与“versicolor”(将后两类均看做第2类)，那么数据按照特征：花瓣长度与宽度做分类。

感知机分类实例：

a<-0.2
w<-rep(0,3)
iris1<-t(as.matrix(iris[,3:4]))
d<-c(rep(0,50),rep(1,100))
e<-rep(0,150)
p<-rbind(rep(1,150),iris1)
max<-100000
eps<-rep(0,100000)
i<-0
repeat{
  v<-w%*%p;
  y<-ifelse(sign(v)>=0,1,0);
  e<-d-y;
  eps[i+1]<-sum(abs(e))/length(e)
  if(eps[i+1]<0.01){
    print("finish:");
    print(w);
    break;
  }
  w<-w+a*(d-y)%*%t(p);
  i<-i+1;
  if(i>max){
    print("max time loop");
    print(eps[i])
    print(y);
    break;
  }
}

输出结果：

[1] "finish:"
           Petal.Length Petal.Width
[1,] -39.6        10.82       18.82

绘图程序：

plot(Petal.Length~Petal.Width,xlim=c(0,3),ylim=c(0,8),
     data=iris[iris$Species=="virginica",])
data1<-iris[iris$Species=="versicolor",]
points(data1$Petal.Width,data1$Petal.Length,col=2)
data2<-iris[iris$Species=="setosa",]
points(data2$Petal.Width,data2$Petal.Length,col=3)
x<-seq(0,3,0.01)
y<-x*(-w[2]/w[3])-w[1]/w[3]
lines(x,y,col=4)
#绘制每次迭代的平均绝对误差
plot(1:i,eps[1:i],type="o")

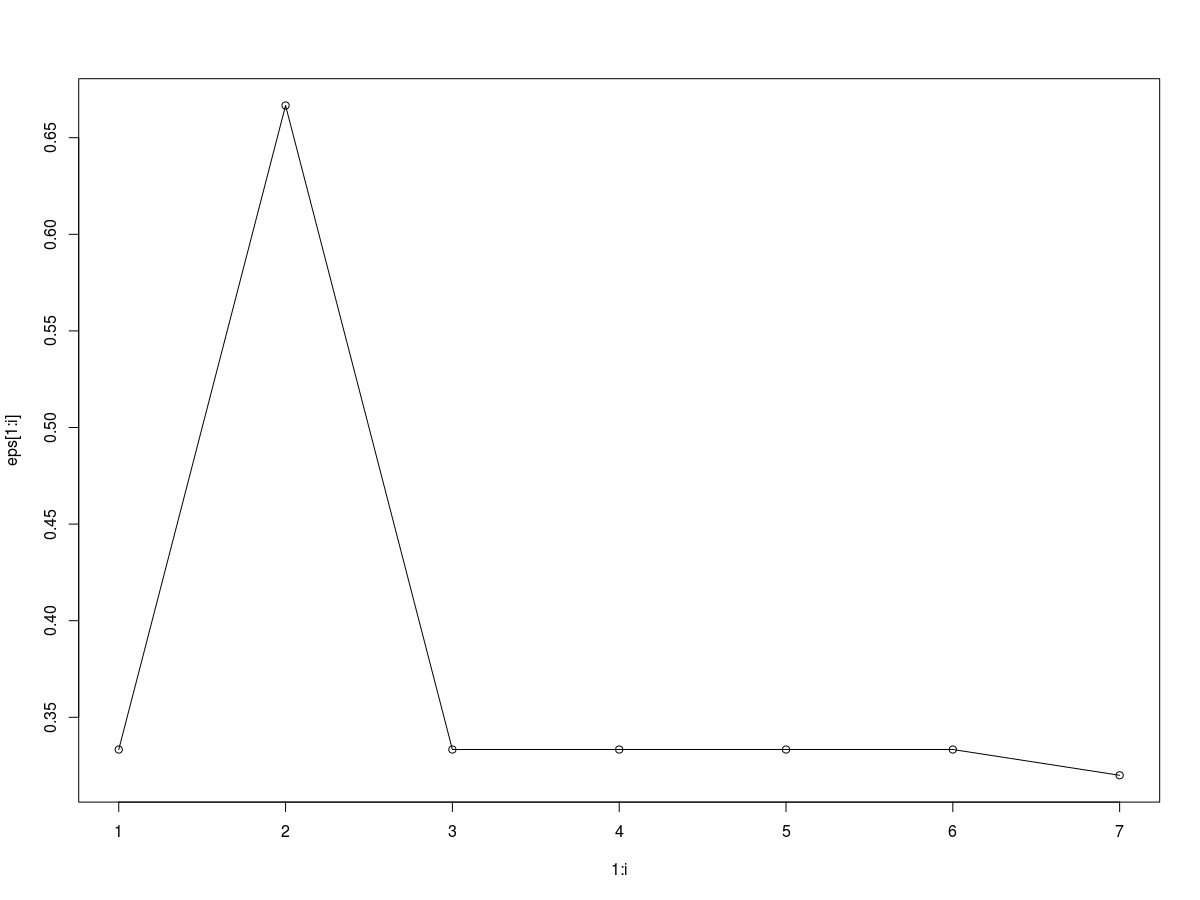这是运行了7次得到的结果。与我们前面的支持向量机相比，显然神经网络的单层感知器分类不是那么的可信，有些弱。

单层的前向神经网络模型在包nnet中的nnet函数，其调用格式为：

nnet(formula,data, weights, size, Wts, linout = F, entropy = F,softmax = F, skip = F, rang = 0.7,decay = 0, maxit = 100,trace = T)

参数说明:

size, 隐层结点数;

decay, 表明权值是递减的(可以防止过拟合);

linout, 线性输出单元开关;

skip，是否允许跳过隐层;

maxit, 最大迭代次数;

Hess, 是否输出Hessian值

适用于神经网络的方法有predict,print和summary等，nnetHess函数用来计算在考虑了权重参数下的Hessian矩阵，并且检验是否是局部最小。

我们使用nnet函数分析Vehicle数据。随机选择半数观测作为训练集，剩下的作为测试集，构建只有包含3个节点的一个隐藏层的神经网络。输入如下程序：


library(nnet); #安装nnet软件包 
library(mlbench); #安装mlbench软件包
data(Vehicle); #调入数据
n=length(Vehicle[,1]); #样本量
set.seed(1); #设随机数种子
samp=sample(1:n,n/2); #随机选择半数观测作为训练集
b=class.ind(Vehicle$Class); #生成类别的示性函数
test.cl=function(true,pred){true<-max.col(true);cres=max.col(pred);table(true,cres)};
#利用训练集中前18个变量作为输入变量，隐藏层有3个节点，初始随机权值在[-0.1,0.1]，权值是逐渐衰减的。
a=nnet(Vehicle[samp,-19],b[samp,],size=3,rang=0.1,decay=5e-4,maxit=200); 
test.cl(b[samp,],predict(a,Vehicle[samp,-19]))#给出训练集分类结果
test.cl(b[-samp,],predict(a,Vehicle[-samp,-19]));#给出测试集分类结果
#构建隐藏层包含15个节点的网络。接着上面的语句输入如下程序：
a=nnet(Vehicle[samp,-19],b[samp,],size=15,rang=0.1,decay=5e-4,maxit=10000);
test.cl(b[samp,],predict(a,Vehicle[samp,-19]));
test.cl(b[-samp,],predict(a,Vehicle[-samp,-19]));

3个节点神经网络输出结果：

# weights:  73
initial  value 423.287179 
iter  10 value 316.056828
iter  20 value 315.921050
iter  30 value 315.858894
iter  40 value 315.828441
iter  50 value 315.654455
iter  60 value 314.025009
iter  70 value 293.078336
iter  80 value 272.137131
iter  90 value 256.349423
iter 100 value 245.067673
iter 110 value 227.302736
iter 120 value 216.378426
iter 130 value 208.730935
iter 140 value 205.731594
iter 150 value 202.190641
iter 160 value 183.854358
iter 170 value 175.801334
iter 180 value 174.550935
iter 190 value 171.361604
iter 200 value 168.915354
final  value 168.915354 
stopped after 200 iterations

3个节点隐藏层训练集分类结果：

cres
true   1   2   3   4
   1  96   7   0   7
   2   4 103   2   2
   3   8 103   1   5
   4   4   0   0  81

3个节点隐藏层测试集分类结果：

cres
true   1   2   3   4
   1  83  12   1  12
   2   4  93   1   3
   3   9  86   1   4
   4   8   3   2 101

15个节点隐藏层训练集分类结果：

cres
true   1   2   3   4
   1 110   0   0   0
   2   0 111   0   0
   3   0   0 117   0
   4   0   0   0  85

15个节点隐藏层测试集分类结果：

cres
true   1   2   3   4
   1  98   2   6   2
   2   0  69  32   0
   3   0  34  66   0
   4   1   5   5 103

四 常见问题

  1. 多层感知机如何解决回归问题？
    多层感知机最初是为了做分类的，但是它也可以处理回归问题，只要在最后将softmax等分类器改成sigmoid回归就行。

  2. 多层感知机的隐层作用？

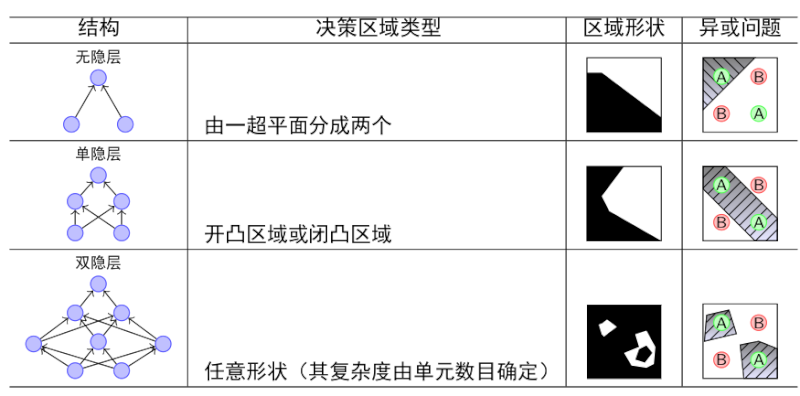
  3. MLP的缺陷？
    1.网络的隐含节点个数选取问题至今仍是一个世界难题（Google,
    Elsevier, CNKI）；

    2.停止阈值、学习率、动量常数需要采用”trial-and-error”法，极其耗时（动手实验）；

    3.学习速度慢；

    4.容易陷入局部极值，学习不够充分。

results matching ""

    No results matching ""