实验一:KNN分类实验
一 实验目的
- 了解KNN算法的基本思想,学习基于实例的学习
- 了解KNN算法原理,优缺点以及使用技巧
- 学会使用Python建立KNN分类模型
二 实验原理
KNN是k nearest neighbor 的简称,即k最邻近,就是找k个最近的实例投票决定新实例的类标。KNN是一种基于实例的学习算法,它不同于贝叶斯、决策树等算法,KNN不需要训练,当有新的实例出现时,直接在训练数据集中找k个最近的实例,把这个新的实例分配给这k个训练实例中实例数最多类。KNN也称为懒惰学习,它不需要训练过程,在类标边界比较整齐的情况下分类的准确率很高。KNN算法需要人为决定K的取值,即找几个最近的实例,k值不同,分类结果的结果也会不同。
基于实例的学习
存储所有实验用例,当有分类请求时,根据查询实例和已有实例的关系进行局部计算分类。不会有全局性的计算函数。归纳偏置是实例分布在欧式空间里是平滑的。
KNN简单例子:
看如下图的训练数据集的分布,该数据集分为3类(在图中以三种不同的颜色表示),现在出现一个待分类的新实例(图中绿色圆点),假设我们的K=3,即找3个最近的实例,这里的定义的距离为欧氏距离,这样找据该待分类实例最近的三个实例就是以绿点为中心画圆,确定一个最小的半径,使这个圆包含K个点。
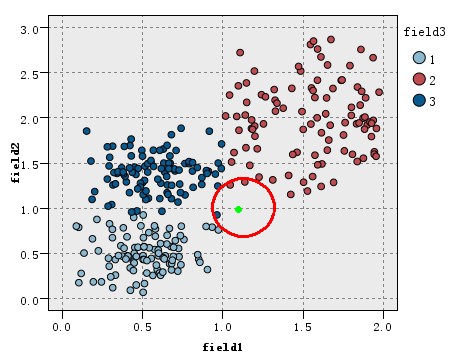
算法:
训练样本是多维特征空间向量,其中每个训练样本带有一个类别标签。算法的训练阶段只包含存储的特征向量和训练样本的标签。在分类阶段,k是一个用户定义的常数。一个没有类别标签的向量(查询或测试点)将被归类为最接近该点的k个样本点中最频繁使用的一类。一般情况下,将欧氏距离作为距离度量,但是这是只适用于连续变量。在文本分类这种离散变量情况下,另一个度量——重叠度量(或海明距离)可以用来作为度量。
参数选择:
如何选择一个最佳的K值取决于数据。一般情况下,在分类时较大的K值能够减小噪声的影响,但会使类别之间的界限变得模糊,造成欠拟合。而较小的K值会过拟合。一个较好的K值能通过各种启发式技术来获取。在二元(两类)分类问题中,选取k为奇数有助于避免两个分类平票的情形。
三 实验步骤
装载我们需要的数据包:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
定义邻居个数为15,当然你也可以取其他值:
n_neighbors = 15
载入iris数据集
iris = datasets.load_iris()
本案例中,我们仅仅使用两个特征,你可以尝试自己选择:
X = iris.data[:, :2]
y = iris.target
h = .02 # step size in the mesh
创建颜色对,用于之后可视化:
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
循环实现逻辑:
for weights in ['uniform', 'distance']:
# we create an instance of Neighbours Classifier and fit the data.
clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
clf.fit(X, y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = %i, weights = '%s')"
% (n_neighbors, weights))
画图展示:
plt.show()
你可以得到以下图片:
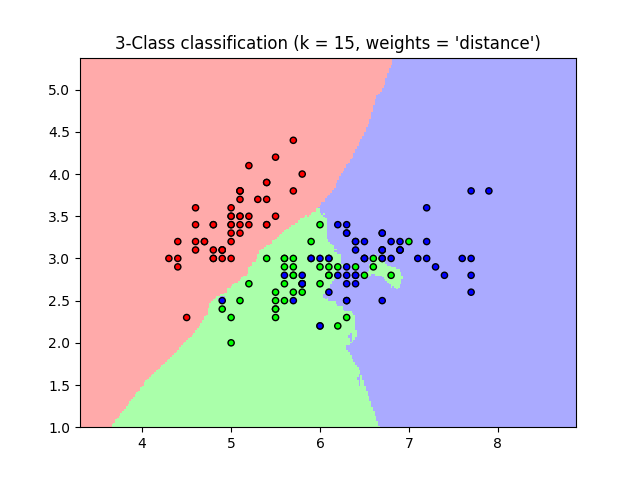
四 常见问题
K值设定你需要掌握为多大?
k太小,分类结果易受噪声点影响;k太大,近邻中又可能包含太多的其它类别的点。(对距离加权,可以降低k值设定的影响)。k值通常是采用交叉检验来确定(以k=1为基准.经验规则:k一般低于训练样本数的平方根。类别如何判定最合适?
投票法没有考虑近邻的距离的远近,距离更近的近邻也许更应该决定最终的分类,所以加权投票法更恰当一些。如何选择合适的距离度量?
高维度对距离衡量的影响:众所周知当变量数越多,欧式距离的区分能力就越差。变量值域对距离的影响:值域越大的变量常常会在距离计算中占据主导作用,因此应先对变量进行标准化。训练样本是否要一视同仁?
在训练集中,有些样本可能是更值得依赖的。可以给不同的样本施加不同的权重,加强依赖样本的权重,降低不可信赖样本的影响。性能问题?
kNN是一种懒惰算法,平时不好好学习,考试(对测试样本分类)时才临阵磨枪(临时去找k个近邻)。懒惰的后果:构造模型很简单,但在对测试样本分类地的系统开销大,因为要扫描全部训练样本并计算距离。已经有一些方法提高计算的效率,例如压缩训练样本量等。