实验目的
了解分类预测的基本流程,并掌握R语言实现分类算法的基本方法
实验原理
分类是数据挖掘中应用领域极其广泛的重要技术之一,至今已经提出很多算法。分类是根据数据集的特点构造一个分类器,利用分类器对未知类别的样本赋予类别的一种技术。构造分类器的过程一般分为训练和测试两个步骤。在训练阶段,分析训练数据集的特点,为每个类别产生一个对相应数据集的准确描述或模型。在测试阶段,利用类别的描述或模型对测试进行分类,测试其分类准确度。
本节教程使用k-近邻(knn)算法作为例子解释R语言中实现分类算法的基本流程。
k-近邻(kNN,k-Nearest Neighbors)算法是一种基于实例的分类方法。该方法就是找出与未知样本x距离最近的k个训练样本,看这k个样本中多数属于哪一类,就把x归为那一类。k-近邻方法是一种懒惰学习方法,它存放样本,直到需要分类时才进行分类,如果样本集比较复杂,可能会导致很大的计算开销,因此无法应用到实时性很强的场合。
K值大小的选取会对K近邻算法的结果会产生重大影响。如果选择较小的K值,就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是“学习”的估计误差会增大,换句话说,K值的减小就意味着整体模型变得复杂,容易发生过拟合;如果选择较大的K值,就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误。在实际应用中,K值一般取一个比较小的数值,例如采用交叉验证法(简单来说,就是一部分样本做训练集,一部分做测试集)来选择最优的K值。
实验步骤
我们使用R语言中的kknn()函数对iris数据集进行knn算法的实现。
首先安装kknn包并加载
> install.packages("kknn")
> library(kknn)
加载iris数据集,并生成采样数据,将iris数据集分为两部分,分别为训练数据集iris.learn和测试数据集iris.valid
> m <- dim(iris)[1]
> val <- sample(1:m, size = round(m/3), replace = FALSE, prob = rep(1/m, m))
> iris.learn <- iris[-val,]
> iris.valid <- iris[val,]
调用kknn()函数
> iris.kknn <- kknn(Species~., iris.learn, iris.valid, distance = 1, kernel = "triangular")
> summary(iris.kknn)
Call:
kknn(formula = Species ~ ., train = iris.learn, test = iris.valid, distance = 1, kernel = "triangular")
Response: "nominal"
fit prob.setosa prob.versicolor prob.virginica
1 virginica 0 0.00000000 1.00000000
2 virginica 0 0.01624687 0.98375313
3 versicolor 0 1.00000000 0.00000000
4 virginica 0 0.10041431 0.89958569
5 versicolor 0 1.00000000 0.00000000
6 virginica 0 0.00000000 1.00000000
7 versicolor 0 1.00000000 0.00000000
8 versicolor 0 1.00000000 0.00000000
9 setosa 1 0.00000000 0.00000000
10 versicolor 0 0.83072576 0.16927424
11 setosa 1 0.00000000 0.00000000
12 setosa 1 0.00000000 0.00000000
13 virginica 0 0.00000000 1.00000000
14 virginica 0 0.07954460 0.92045540
15 versicolor 0 1.00000000 0.00000000
16 versicolor 0 1.00000000 0.00000000
17 virginica 0 0.00000000 1.00000000
18 setosa 1 0.00000000 0.00000000
19 virginica 0 0.10028773 0.89971227
20 virginica 0 0.00000000 1.00000000
21 versicolor 0 1.00000000 0.00000000
22 versicolor 0 1.00000000 0.00000000
23 virginica 0 0.00000000 1.00000000
24 setosa 1 0.00000000 0.00000000
25 versicolor 0 0.68610975 0.31389025
26 versicolor 0 0.77887494 0.22112506
27 versicolor 0 1.00000000 0.00000000
28 setosa 1 0.00000000 0.00000000
29 setosa 1 0.00000000 0.00000000
30 virginica 0 0.24798470 0.75201530
31 setosa 1 0.00000000 0.00000000
32 versicolor 0 0.96768116 0.03231884
33 versicolor 0 1.00000000 0.00000000
34 setosa 1 0.00000000 0.00000000
35 setosa 1 0.00000000 0.00000000
36 setosa 1 0.00000000 0.00000000
37 virginica 0 0.00000000 1.00000000
38 setosa 1 0.00000000 0.00000000
39 virginica 0 0.00000000 1.00000000
40 setosa 1 0.00000000 0.00000000
41 setosa 1 0.00000000 0.00000000
42 virginica 0 0.10639202 0.89360798
43 versicolor 0 1.00000000 0.00000000
44 setosa 1 0.00000000 0.00000000
45 versicolor 0 0.96070841 0.03929159
46 setosa 1 0.00000000 0.00000000
47 versicolor 0 1.00000000 0.00000000
48 virginica 0 0.13230826 0.86769174
49 virginica 0 0.00000000 1.00000000
50 versicolor 0 1.00000000 0.00000000
使用交叉验证法查看测试数据集分类情况
> fit <- fitted(iris.kknn)
> table(iris.valid$Species, fit)
fit
setosa versicolor virginica
setosa 14 0 0
versicolor 0 15 1
virginica 0 2 18
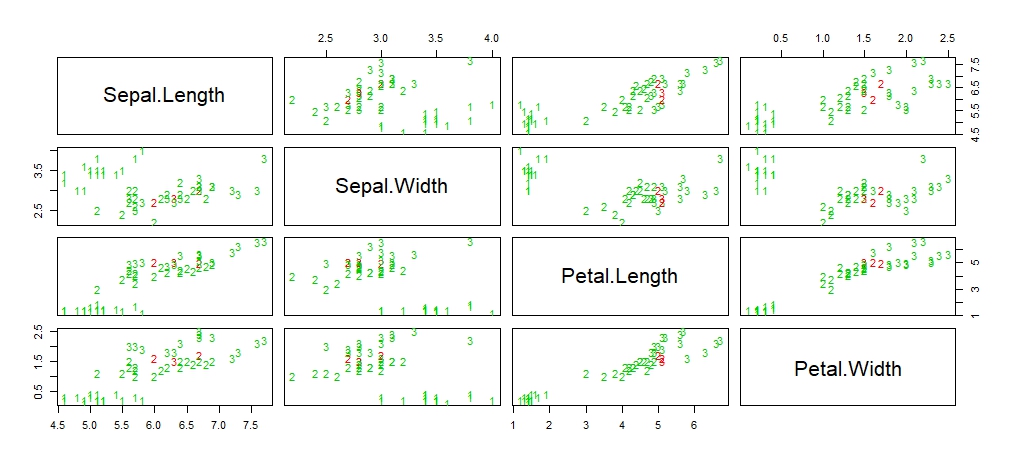
绘制测试数据集的散点矩阵图,其中错误分类样本用红色标注
> pcol <- as.character(as.numeric(iris.valid$Species))
> pairs(iris.valid[1:4], pch = pcol, col = c("green3", "red")[(iris.valid$Species != fit)+1])