实验二：支持向量机分类实验
一 实验目的
- 了解支持向量机的基本原理，几何间隔函数间隔等基础概念
- 了解支持向量机的优缺点和适用场景
- 学会使用R语言建立SVM分类模型
二 实验原理
支持向量机（support vector machines，SVM)是一种二类分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；支持向量机还包括核技巧，这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化，可形式化为一个求解凸二次规划（convex quadratic programming，不怕，附录有解释)的问题，也等价于正则化的合页损失函数（后面也有解释）的最小化问题。支持向量机的学习算法是求解凸二次规划的最优化算法。
下文将带您学习到支持向量机如何工作，以及如何利用R语言实现支持向量机分类算法。
线性分类
下面举个简单的例子，如下图所示，现在有一个二维平面，平面上有两种不同的数据，分别用圈和叉表示。由于这些数据是线性可分的，所以可以用一条直线将这两类数据分开，这条直线就相当于一个超平面，超平面一边的数据点所对应的y全是 -1 ，另一边所对应的y全是1。
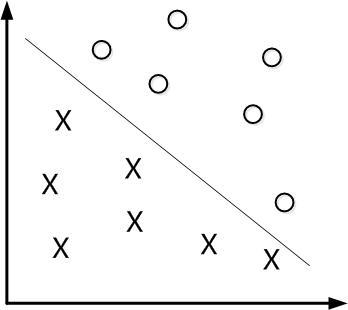
这个超平面可以用分类函数
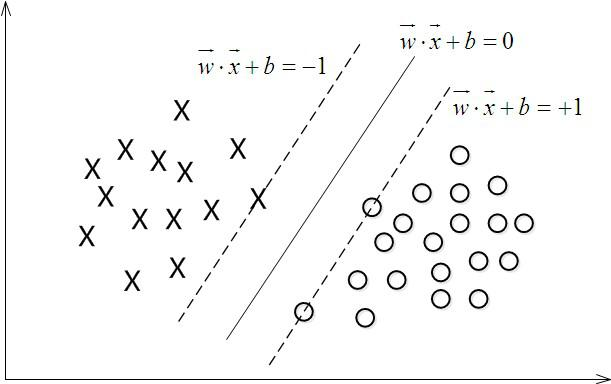
函数间隔与几何间隔
在超平面w*x+b=0确定的情况下，|w*x+b|能够表示点x到距离超平面的远近，而通过观察w*x+b的符号与类标记y的符号是否一致可判断分类是否正确，所以，可以用(y*(w*x+b))的正负性来判定或表示分类的正确性。于此，我们便引出了函数间隔（functional margin）的概念。
定义函数间隔（用
而超平面(w，b)关于T中所有样本点(xi，yi)的函数间隔最小值（其中，x是特征，y是结果标签，i表示第i个样本），便为超平面(w, b)关于训练数据集T的函数间隔：
但这样定义的函数间隔有问题，即如果成比例的改变w和b（如将它们改成2w和2b），则函数间隔的值f(x)却变成了原来的2倍（虽然此时超平面没有改变），所以只有函数间隔还远远不够。事实上，我们可以对法向量w加些约束条件，从而引出真正定义点到超平面的距离--几何间隔（geometrical margin）的概念。假定对于一个点 x ，令其垂直投影到超平面上的对应点为 x0 ，w 是垂直于超平面的一个向量，
有
又由于 x0 是超平面上的点，满足 f(x0)=0 ，代入超平面的方程
最大间隔分类器
对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的确信度（confidence）也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。这个间隔如下图中的gap / 2所示。
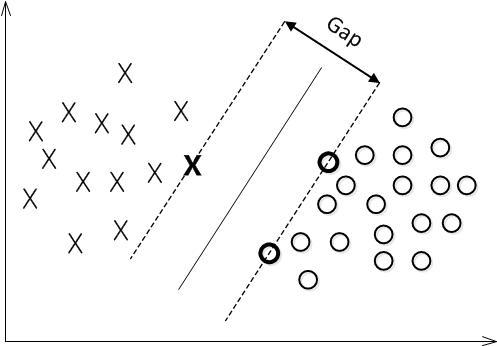
通过由前面的分析可知：函数间隔不适合用来最大化间隔值，因为在超平面固定以后，可以等比例地缩放w的长度和b的值，这样可以使得
，使得在缩放w和b的时候几何间隔
于是最大间隔分类器（maximum margin classifier）的目标函数可以定义为：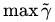
同时需满足一些条件，根据间隔的定义，有
其中，s.t.，即subject to的意思，它导出的是约束条件。回顾下几何间隔的定义
这个目标函数便是在相应的约束条件
如下图所示，中间的实线便是寻找到的最优超平面（Optimal Hyper Plane），其到两条虚线的距离相等，这个距离便是几何间隔
三 实验步骤
让我们看一下如何使用支持向量机实现二元分类器，使用的数据是来自MASS包的cats数据集。在本例中你将尝试使用体重和心脏重量来预测一只猫的性别。我们拿数据集中20%的数据点，用于测试模型的准确性（在其余的80%的数据上建立模型）。
#安装本次程序需要的数据包
install.packages("MASS")
install.packages("e1071")
# Setup
library(e1071)
data(cats, package="MASS")
inputData <- data.frame(cats[, c (2,3)], response = as.factor(cats$Sex)) # response as factor
线性支持向量机
传递给函数svm()的关键参数是kernel、cost和gamma。Kernel指的是支持向量机的类型，它可能是线性SVM、多项式SVM、径向SVM或Sigmoid SVM。Cost是违反约束时的成本函数，gamma是除线性SVM外其余所有SVM都使用的一个参数。还有一个类型参数，用于指定该模型是用于回归、分类还是异常检测。但是这个参数不需要显式地设置，因为支持向量机会基于响应变量的类别自动检测这个参数，响应变量的类别可能是一个因子或一个连续变量。所以对于分类问题，一定要把你的响应变量作为一个因子。
# linear SVM
svmfit <- svm(response ~ ., data = inputData, kernel = "linear", cost = 10, scale = FALSE) # linear svm, scaling turned OFF
print(svmfit)
plot(svmfit, inputData)
compareTable <- table (inputData$response, predict(svmfit)) # tabulate
mean(inputData$response != predict(svmfit)) # 19.44% misclassification error
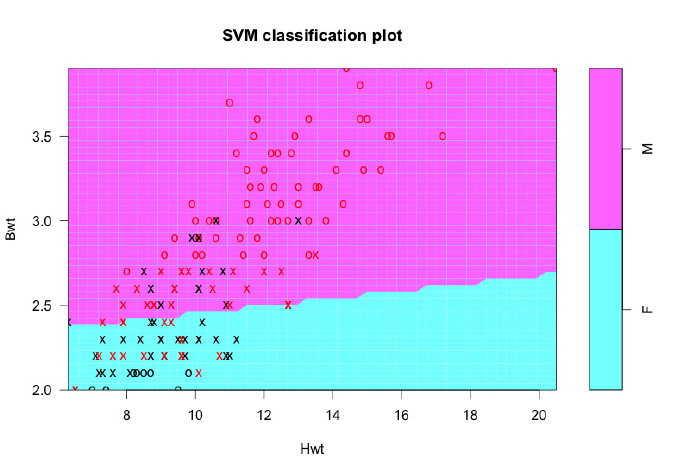
径向支持向量机
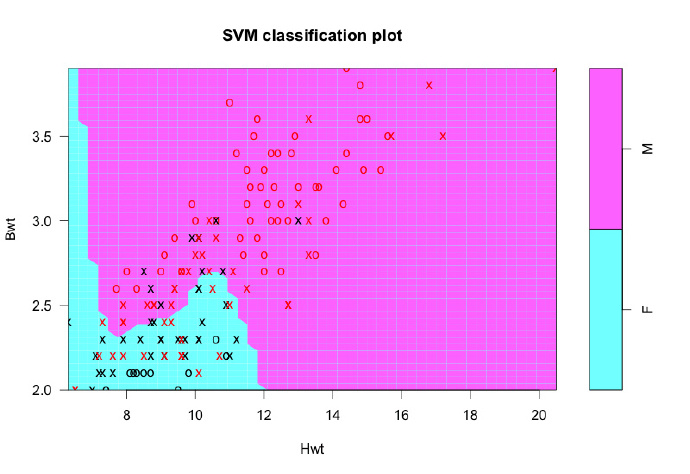
径向基函数作为一个受欢迎的内核函数，可以通过设置内核参数作为“radial”来使用。当使用一个带有“radial”的内核时，结果中的超平面就不需要是一个线性的了。通常定义一个弯曲的区域来界定类别之间的分隔，这也往往导致相同的训练数据，更高的准确度。
# radial SVM
svmfit <- svm(response ~ ., data = inputData, kernel = "radial", cost = 10, scale = FALSE) # radial svm, scaling turned OFF
print(svmfit)
plot(svmfit, inputData)
compareTable <- table (inputData$response, predict(svmfit)) # tabulate
mean(inputData$response != predict(svmfit)) # 18.75% misclassification error
寻找最优参数
你可以使用tune.svm()函数，来寻找svm()函数的最优参数。
### Tuning
# Prepare training and test data
set.seed(100) # for reproducing results
rowIndices <- 1 : nrow(inputData) # prepare row indices
sampleSize <- 0.8 * length(rowIndices) # training sample size
trainingRows <- sample (rowIndices, sampleSize) # random sampling
trainingData <- inputData[trainingRows, ] # training data
testData <- inputData[-trainingRows, ] # test data
tuned <- tune.svm(response ~., data = trainingData, gamma = 10^(-6:-1), cost = 10^(1:2)) # tune
summary (tuned) # to select best gamma and cost
# Parameter tuning of 'svm':
# - sampling method: 10-fold cross validation
#
# - best parameters:
# gamma cost
# 0.001 100
#
# - best performance: 0.26
#
# - Detailed performance results:
# gamma cost error dispersion
# 1 1e-06 10 0.36 0.09660918
# 2 1e-05 10 0.36 0.09660918
# 3 1e-04 10 0.36 0.09660918
# 4 1e-03 10 0.36 0.09660918
# 5 1e-02 10 0.27 0.20027759
# 6 1e-01 10 0.27 0.14944341
# 7 1e-06 100 0.36 0.09660918
# 8 1e-05 100 0.36 0.09660918
# 9 1e-04 100 0.36 0.09660918
# 10 1e-03 100 0.26 0.18378732
# 11 1e-02 100 0.26 0.17763883
# 12 1e-01 100 0.26 0.15055453
结果证明，当cost为100，gamma为0.001时产生最小的错误率。利用这些参数训练径向支持向量机。
svmfit <- svm (response ~ ., data = trainingData, kernel = "radial", cost = 100, gamma=0.001, scale = FALSE) # radial svm, scaling turned OFF
print(svmfit)
plot(svmfit, trainingData)
compareTable <- table (testData$response, predict(svmfit, testData)) # comparison table
mean(testData$response != predict(svmfit, testData)) # 13.79% misclassification error
F M
F 6 3
M 1 19
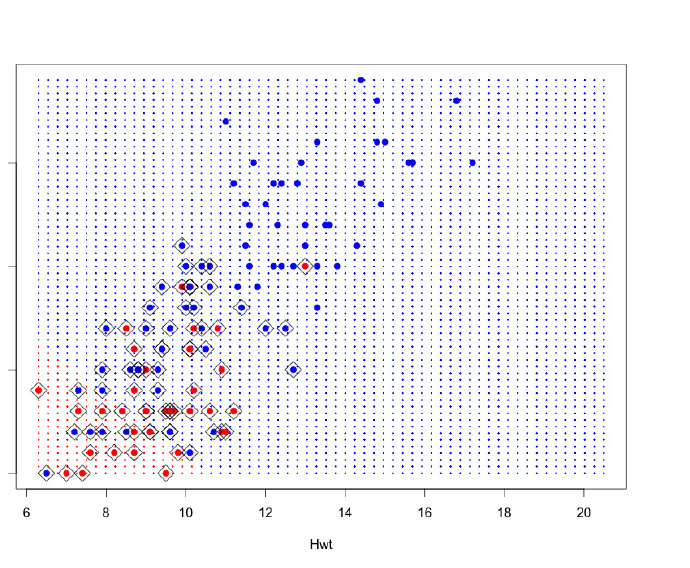
网格图
一个2-色的网格图，能让结果看起来更清楚，它将图的区域指定为利用SVM分类器得到的结果的类别。在下边的例子中，这样的网格图中有很多数据点，并且通过数据点上的倾斜的方格来标记支持向量上的点。很明显，在这种情况下，有很多越过边界违反约束的点，但在SVM内部它们的权重都被降低了。
# Grid Plot
n_points_in_grid = 60 # num grid points in a line
x_axis_range <- range (inputData[, 2]) # range of X axis
y_axis_range <- range (inputData[, 1]) # range of Y axis
X_grid_points <- seq (from=x_axis_range[1], to=x_axis_range[2], length=n_points_in_grid) # grid points along x-axis
Y_grid_points <- seq (from=y_axis_range[1], to=y_axis_range[2], length=n_points_in_grid) # grid points along y-axis
all_grid_points <- expand.grid (X_grid_points, Y_grid_points) # generate all grid points
names (all_grid_points) <- c("Hwt", "Bwt") # rename
all_points_predited <- predict(svmfit, all_grid_points) # predict for all points in grid
color_array <- c("red", "blue")[as.numeric(all_points_predited)] # colors for all points based on predictions
plot (all_grid_points, col=color_array, pch=20, cex=0.25) # plot all grid points
points (x=trainingData$Hwt, y=trainingData$Bwt, col=c("red", "blue")[as.numeric(trainingData$response)], pch=19) # plot data points
points (trainingData[svmfit$index, c (2, 1)], pch=5, cex=2) # plot support vectors
四 常见问题：
支持向量机如何工作？
简单介绍下支持向量机是做什么的：假设你的数据点分为两类，支持向量机试图寻找最优的一条线（超平面），使得离这条线最近的点与其他类中的点的距离最大。有些时候，一个类的边界上的点可能越过超平面落在了错误的一边，或者和超平面重合，这种情况下，需要将这些点的权重降低，以减小它们的重要性。这种情况下，“支持向量”就是那些落在分离超平面边缘的数据点形成的线
无法确定分类线（线性超平面）时该怎么办？
此时可以将数据点投影到一个高维空间，在高维空间中它们可能就变得线性可分了。它会将问题作为一个带约束的最优化问题来定义和解决，其目的是为了最大化两个类的边界之间的距离。我的数据点多于两个类时该怎么办？
此时支持向量机仍将问题看做一个二元分类问题，但这次会有多个支持向量机用来两两区分每一个类，直到所有的类之间都有区别。