实验目的

掌握R语言中箱线图的绘制

实验原理

箱线图（又称盒须图）通过绘制连续型变量的五数总括，即最小值、下四分位数（第25百分位数）、中位数（第50百分位数）、上四分位数（第75百分位数）以及最大值，描述了连续型变量的分布。箱线图能够显示可能为离群点（范围±1.5*IQR以外的值，IQR表示四分位距，即上四分位数与下四分位数的差值）的观测。

实验步骤

下面的例子描绘了美国一家航空公司在1949年到1960年每年的航空乘客数量，该数据集名为AirPassengers，是R自带数据集，其中横坐标表示年份，纵坐标为每年各月份的乘客数量。

> library(ggplot2)
> ggplot(data=AirPassengers_modified,aes(group=year,x=year,y=x))+geom_point(aes(color=factor(year)),
alpha=0.2,position="jitter")+geom_boxplot(outlier.size=0, alpha=0.1) +guides(colour=FALSE) 
+ labs(title="每年乘客数量箱线图",x="年份")

抖动散点图被覆盖在箱线图之下。箱子区域包含了50%的点，箱子里的线代表中位数所在的位置，箱子的上边和下边分别代表第一四分位数和第三四分位数所的位置。穿过箱子的线的上端表示距箱子上边1.5*IQR(Q3-Q1)处，线的下端表示距箱子下边1.5*IQR处，一般，在线外的点就可以认为是异常值了。

下面使用boxplot()函数绘制箱线图：

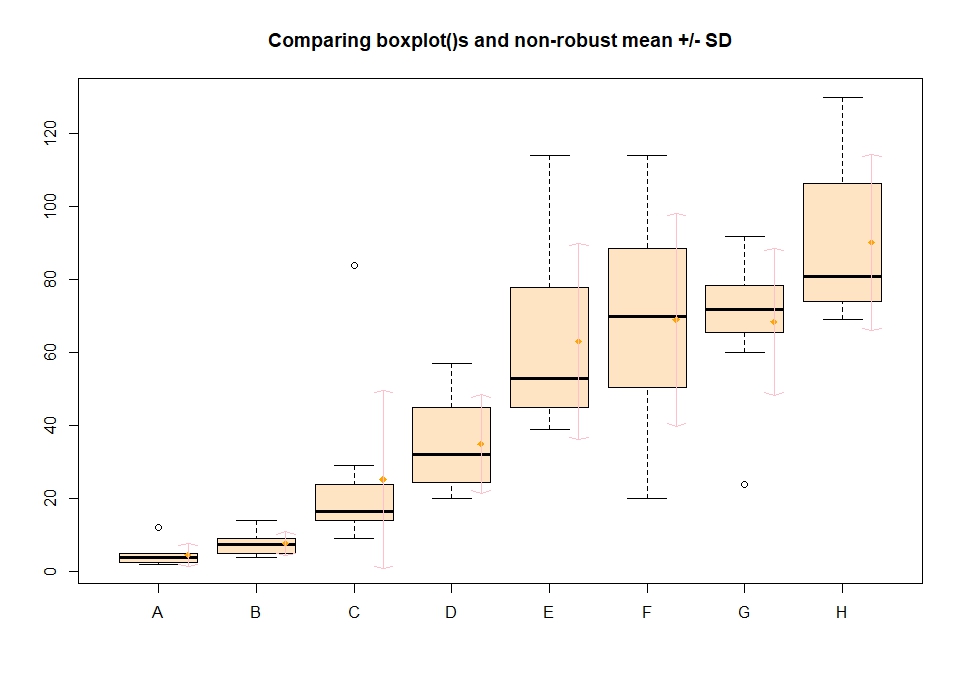
> mn.t <- tapply(OrchardSprays$decrease, OrchardSprays$treatment, mean)
> sd.t <- tapply(OrchardSprays$decrease, OrchardSprays$treatment, sd)
> xi <- 0.3 + seq(rb$n)
> points(xi, mn.t, col = "orange", pch = 18)
> arrows(xi, mn.t - sd.t, xi, mn.t + sd.t,
+        code = 3, col = "pink", angle = 75, length = .1)

另一个例子：

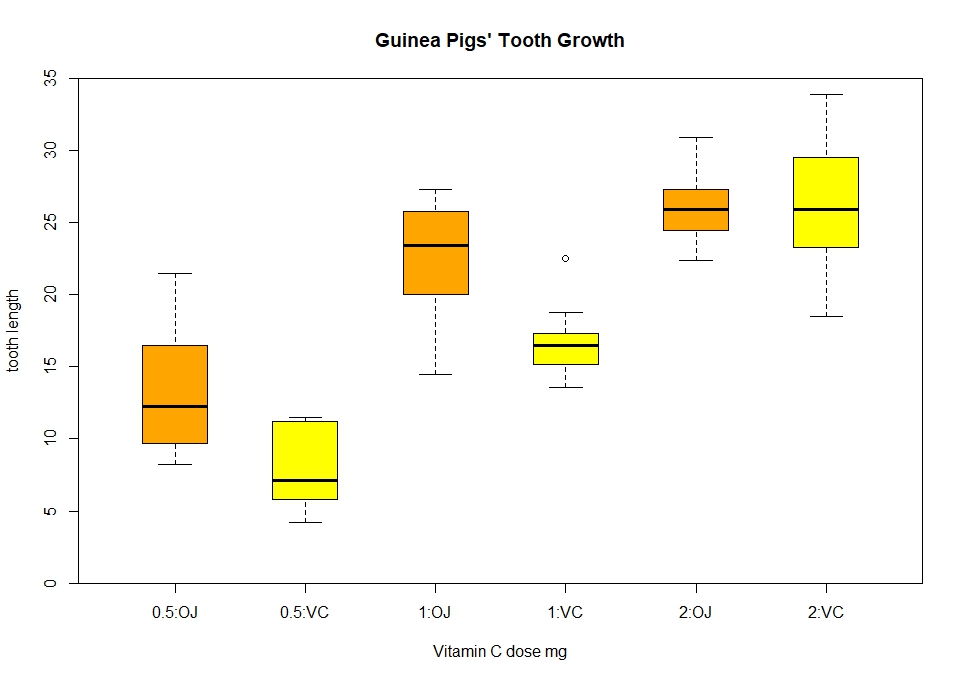
> boxplot(len ~ dose:supp, data = ToothGrowth,
+         boxwex = 0.5, col = c("orange", "yellow"),
+         main = "Guinea Pigs' Tooth Growth",
+         xlab = "Vitamin C dose mg", ylab = "tooth length",
+         sep = ":", lex.order = TRUE, ylim = c(0, 35), yaxs = "i")

绘制散点图并添加标题图例：

> boxplot(len ~ dose:supp, data = ToothGrowth,
+         boxwex = 0.5, col = c("orange", "yellow"),
+         main = "Guinea Pigs' Tooth Growth",
+         xlab = "Vitamin C dose mg", ylab = "tooth length",
+         sep = ":", lex.order = TRUE, ylim = c(0, 35), yaxs = "i")
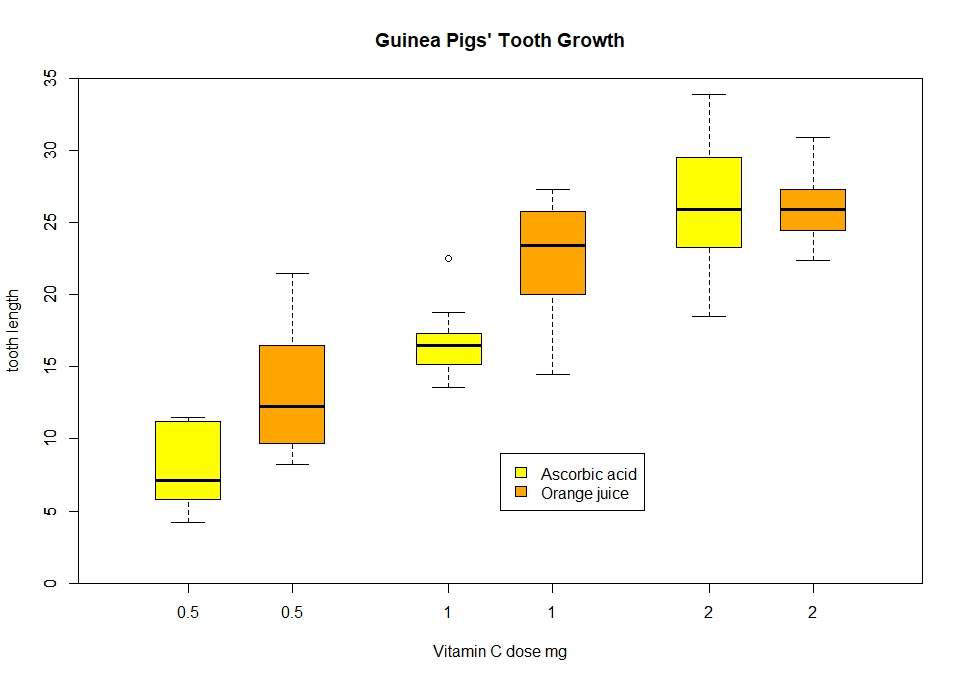
> boxplot(len ~ dose, data = ToothGrowth,
+         boxwex = 0.25, at = 1:3 - 0.2,
+         subset = supp == "VC", col = "yellow",
+         main = "Guinea Pigs' Tooth Growth",
+         xlab = "Vitamin C dose mg",
+         ylab = "tooth length",
+         xlim = c(0.5, 3.5), ylim = c(0, 35), yaxs = "i")
> boxplot(len ~ dose, data = ToothGrowth, add = TRUE,
+         boxwex = 0.25, at = 1:3 + 0.2,
+         subset = supp == "OJ", col = "orange")
> legend(2, 9, c("Ascorbic acid", "Orange juice"),
+        fill = c("yellow", "orange"))