影响学生招生的因素
实验目的
熟悉使用R语言进行大数据综合分析的方法
实验原理
R工具是一套完整的的数据处理计算和制图软件系统。其功能包括:数据存储和处理系统;数组运算工具(其向量、矩阵运算方面功能尤其强大);完整连贯的统计分析工具;优秀的的统计制图功能;简便而强大的的编程语言:可操纵数据的输入和输出以及可实现分支、循环等用户自定义功能。
实验背景
一个教育领域的研究者可能会对GRE(研究生入学考试成绩)、GPA(大学平均绩点),以及研究生学院的名誉感兴趣,因为它们直接影响学校的招生问题。
在本案例中,我们将根据数据集中提供的400名学生的GRE、GPA、所在学校声誉的信息,利用逻辑回归分析并预测影响学校招生的主要原因,借此判断某个学生是否会被学校录取。
逻辑回归,也称之为逻辑模型,是一种广义的线性回归分析模型。用于预测二分结果变量。在逻辑模型当中,输出结果所占的比率就是预测变量的线性组合。本实验将对R语言中逻辑回归模型的使用做详细演示。
实验步骤
- 熟悉R环境;
- 打开R云件环境;
- 在相应编程环境中修改和运行代码;
- 查看结果。
实验一:数据读取
从给出的网址下载数据集:下载 导入数据和必要的包,如提示包不存在可以用install.packages("包名")的方式安装
library(aod)
library(ggplot2)
library(Rcpp)
### read in original dataset
mydata <- read.csv("http://stats.idre.ucla.edu/stat/data/binary.csv") ## view the first few rows of the datahead(mydata)
实验二:数据探索
一个研究者可能会对GRE(研究生入学考试成绩)、GPA(大学平均绩点),以及研究生学院的名誉感兴趣,因为它们影响学校的招生问题。这里,我们用允许/不允许这个二进制结果表示其因变量。
summary(mydata)
## admit gre gpa rank
## Min. :0.000 Min. :220 Min. :2.26 Min. :1.00
## 1st Qu.:0.000 1st Qu.:520 1st Qu.:3.13 1st Qu.:2.00
## Median :0.000 Median :580 Median :3.40 Median :2.00
## Mean :0.318 Mean :588 Mean :3.39 Mean :2.48
## 3rd Qu.:1.000 3rd Qu.:660 3rd Qu.:3.67 3rd Qu.:3.00
## Max. :1.000 Max. :800 Max. :4.00 Max. :4.00
这个数据集有二进制的结果(输出值,依赖),它表示允许。这里有3个预测变量:gre、gpa以及rank。我们把gre和gpa看作是连续变量。rank表示有4个值为1。这里,为0的那所学校声望最高,其它的这4所高校声望最低。这时,我们可以用summary()函数来汇总一下这个数据集的情况。
实验三:数据预处理
sum(is.na(mydata))
[1] 0
发现没有缺失值。
实验四:分析建模
接下来的代码,通过使用glm()函数(广义线性模型)进行相关评估。首先,我们要把rank(秩)转换成因子,并预示着rank在这里被视为分类变量。
mydata$rank <- factor(mydata$rank)
mylogit <- glm(admit ~ gre + gpa + rank, data = mydata, family = "binomial")
由于我们得到了模型的名字(mylogit),而R并不会从我们的回归中产生任何输出结果。为了得到结果,我们使用summary()函数进行提取:
summary(mylogit)
##
## Call:
## glm(formula = admit ~ gre + gpa + rank, family = "binomial",
## data = mydata)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.627 -0.866 -0.639 1.149 2.079
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.98998 1.13995 -3.50 0.00047 ***
## gre 0.00226 0.00109 2.07 0.03847 *
## gpa 0.80404 0.33182 2.42 0.01539 *
## rank2 -0.67544 0.31649 -2.13 0.03283 *
## rank3 -1.34020 0.34531 -3.88 0.00010 ***
## rank4 -1.55146 0.41783 -3.71 0.00020 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 499.98 on 399 degrees of freedom
## Residual deviance: 458.52 on 394 degrees of freedom
## AIC: 470.5
##
## Number of Fisher Scoring iterations: 4
1.在上面的结果中,我们首先看到的就是call,这提示我们这时的R在运行什么东西,我们设定了什么选项,等等。
2.接下来,我们看到了偏差残差,用于测量模型的拟合度。这部分的结果显示了这个分布的偏差残差,而针对每个使用在模型里的个案。接下来,我们讨论一下如何汇总偏差估计,从而知道模型的拟合结果。
3.下一部分的结果显示了相关系数,标准误差,z统计量(有时也叫Wald Z统计量),以及它的相关结果。gre和gpa都是同等重要的统计量,并作为rank的3个变量。逻辑回归系数给改变了在预测变量中增加一个单位的输出结果误差。
我们可以调用aod包里的wald.test()函数来测试rank的所有影响。图表里的系数的顺序和模型里的项顺序是一样的。这样很重要,因为wald.test()函数就是基于这些模型的项顺序进行测试的。b提供了系数,而Sigma提供了误差项的方差协方差矩阵,而且最终,这些项告诉R哪些项用来进行测试,而在这种情况下,第4、5、6这三项作为rank的层次进行测试。
wald.test(b = coef(mylogit), Sigma = vcov(mylogit), Terms = 4:6)
## Wald test:
## ----------
##
## Chi-squared test:
## X2 = 20.9, df = 3, P(> X2) = 0.00011
卡方检验算出来的值是20.9,这里涉及到3个自由度,p值算出来是0.00011,这预示着我们所假设的这些项之间具有显著的影响效果。
你也可以使用预测概率来帮助你解读这个模型。预测概率可以由分类预测变量或连续预测变量计算出来。为了算出预测概率,我们首先要创建含有我们需要的独立变量来创建新的数据框。
我们将要开始计算每个rank值的预测概率的允许值,并计算gre和gpa的平均值。首先,我们要创建新的数据框:
newdata1 <- with(mydata,
data.frame(gre = mean(gre), gpa = mean(gpa), rank = factor(1:4)))
## view data frame newdata1
## gre gpa rank
newdata1
## 1 588 3.39 1
## 2 588 3.39 2
## 3 588 3.39 3
## 4 588 3.39 4
这些值必须含有和你之前所创建的逻辑回归分析相同的名字(例如,在这个例子中,gre的就必须命名为gre)。既然,我们现在已经创建好了我们需要进行运算的数据框,那么我们可以告诉R根据这个来创建预测概率。第一行代码经过了压缩,我们现在就把它分开来,讨论这些值是怎样执行的。Newdata$rankP告诉R我们要根据数据集(数据框)的newdata1里的rankP创建一个新的变量剩余的指令告诉R这些rankP值应当使用prediction()函数进行预测。圆括号里的选项告诉R这些预测值应该基于分析mylogit进行预测,mylogit的值源自newdata1以及它的预测值类型就是预测概率(type=”response”)。第二行代码列举了数据框newdata1的值,尽管它不是十分理想,而这就是图表的预测概率。
newdata1$rankP <- predict(mylogit, newdata = newdata1, type = "response")
newdata1
## gre gpa rank rankP
## 1 588 3.39 1 0.517
## 2 588 3.39 2 0.352
## 3 588 3.39 3 0.219
## 4 588 3.39 4 0.185
在上面的预测结果中,我们看到来自最好的名校(rank=1)并被接收到研究生的本科生预测概率是0.52,而0.18的学生来自最低档次的学校(rank=4),以gre和gpa作为平均值。我们可以做相似的事情来创建一个针对不断变化的变量gre和gpa的预测概率图表。我们可以基于此作图,所以我们可以在200到800之间创建100个gre值,基于它的rank(1,2,3,4)。
newdata2 <- with(mydata,data.frame(gre = rep(seq(from = 200, to = 800, length.out = 100), 4),gpa = mean(gpa), rank = factor(rep(1:4, each = 100))))
这些代码所产生的预测概率(下面第一行)和之前算的一样,除非我们还想要对标准差进行要求,否则我们可以对置信区间作图。我们可以对关联规模进行预测,同时反向变换预测值和置信区间的临近值到概率中。
newdata3 <- cbind(newdata2, predict(mylogit, newdata = newdata2, type="link", se=TRUE))
newdata3 <- within(newdata3, {
PredictedProb <- plogis(fit)
LL <- plogis(fit - (1.96 * se.fit))
UL <- plogis(fit + (1.96 * se.fit))})
实验五:模型评价与优化
newdata3
## view first few rows of final datasethead(newdata3)
## gre gpa rank fit se.fit residual.scale UL LL PredictedProb
## 1 200 3.39 1 -0.811 0.515 1 0.549 0.139 0.308
## 2 206 3.39 1 -0.798 0.509 1 0.550 0.142 0.311
## 3 212 3.39 1 -0.784 0.503 1 0.551 0.145 0.313
## 4 218 3.39 1 -0.770 0.498 1 0.551 0.149 0.316
## 5 224 3.39 1 -0.757 0.492 1 0.552 0.152 0.319
## 6 230 3.39 1 -0.743 0.487 1 0.553 0.155 0.322
实验六:可视化输出
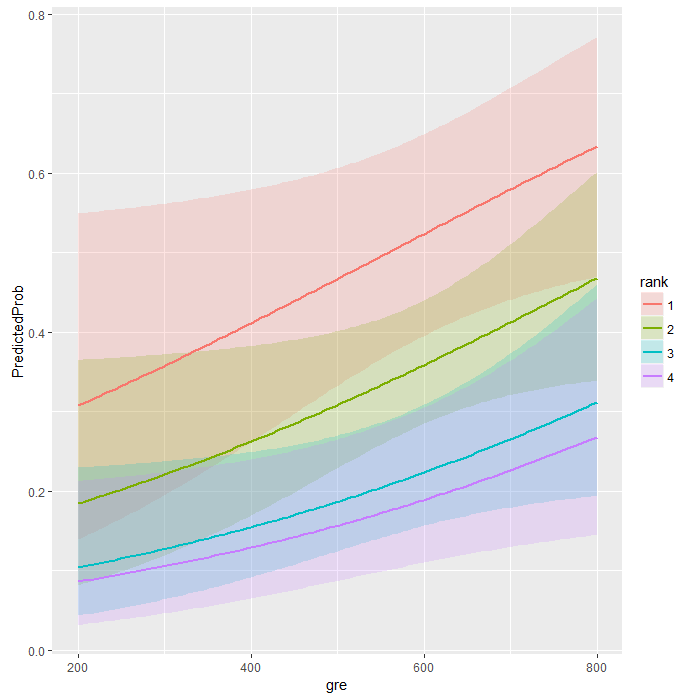
当然,使用图像描绘预测概率来解读和展示模型也是相当有用的。我们会使用ggplot2包来作图。下面我们作图描绘预测概率,和95%置信区间。
ggplot(newdata3, aes(x = gre, y = PredictedProb)) +
geom_ribbon(aes(ymin = LL, ymax = UL, fill = rank), alpha = .2) +
geom_line(aes(colour = rank), size=1)