随机森林分类实验
一 实验目的
- 了解随机森林算法的原理,能够比较决策树和随机森林的相互关系
- 了解模型集成的思想
- 学会使用R语言建立随机森林分类模型
二 实验原理
我们在之前的课程中已经讲解了决策树分类实验,这一节主要讲解由决策树组成的随机森林分类实验。
在随机森林方法中,创建大量的决策树。 每个观察被馈入每个决策树。 每个观察的最常见的结果被用作最终输出。 新的观察结果被馈入所有的树并且对每个分类模型取多数投票。Leo Breiman和Adele Cutler发展出推论出随机森林的算法。而"Random Forests"是他们的商标。这个术语是1995年由贝尔实验室的Tin Kam Ho所提出的随机决策森林(random decision forests)而来的。这个方法则是结合Breimans的"Bootstrap aggregating"想法和Ho的"random subspace method" 以建造决策树的集合。
我们首先介绍随机森林的算法和原理,之后我们给出R语言的使用案例。在R中,“randomForecast”可用于做随机森林的实验。
算法
根据下列算法而建造每棵树:
- 用N来表示训练用例(样本)的个数,M表示特征数目。
- 输入特征数目m,用于确定决策树上一个节点的决策结果;其中m应远小于M。
- 从N个训练用例(样本)中以有放回抽样的方式,取样N次,形成一个训练集(即bootstrap取样),并用未抽到的用例(样本)作预测,评估其误差。
- 对于每一个节点,随机选择m个特征,决策树上每个节点的决定都是基于这些特征确定的。根据这m个特征,计算其最佳的分裂方式。
- 每棵树都会完整成长而不会剪枝(Pruning,这有可能在建完一棵正常树状分类器后会被采用)。
随机森林的优点
- 对于很多种资料,它可以产生高准确度的分类器。
- 它可以处理大量的输入变数。
- 它可以在决定类别时,评估变数的重要性。
- 在建造森林时,它可以在内部对于一般化后的误差产生不偏差的估计。
- 它包含一个好方法可以估计遗失的资料,并且,如果有很大一部分的资料遗失,仍可以维持准确度。
- 它提供一个实验方法,可以去侦测variable interactions。
- 对于不平衡的分类资料集来说,它可以平衡误差。
- 它计算各例中的亲近度,对于数据挖掘、侦测离群点(outlier)和将资料视觉化非常有用。
- 使用上述。它可被延伸应用在未标记的资料上,这类资料通常是使用非监督式聚类。也可侦测偏离者和观看资料。
- 学习过程是很快速的。
随机森林的缺点
- 对小量数据集和低维数据集的分类不一定可以得到很好的效果。
- 执行速度虽然比Boosting等快,但是比单个的决策树慢很多。
- 可能会出现一些差异度非常小的树,淹没了一些正确的决策。
三 实验步骤
安装R包
在R语言控制台中使用以下命令安装软件包。 您还必须安装相关软件包(如果有)。
install.packages("randomForest")
包“randomForest”具有函数randomForest(),用于创建和分析随机森林。
语法
在R语言中创建随机森林的基本语法是 -
randomForest(formula, data)
以下是所使用的参数的描述 -
formula是描述预测变量和响应变量的公式。
data是所使用的数据集的名称。
输入数据
我们将使用名为readingSkills的R语言内置数据集来创建决策树。 它描述了某人的readingSkills的分数,如果我们知道变量“age”,“shoesize”,“score”,以及该人是否是母语。
以下是示例数据。
# Load the party package. It will automatically load other required packages.
library(party)
# Print some records from data set readingSkills.
print(head(readingSkills))
当我们执行上面的代码,它产生以下结果及图表 -
nativeSpeaker age shoeSize score
1 yes 5 24.83189 32.29385
2 yes 6 25.95238 36.63105
3 no 11 30.42170 49.60593
4 yes 7 28.66450 40.28456
5 yes 11 31.88207 55.46085
6 yes 10 30.07843 52.83124
Loading required package: methods
Loading required package: grid
...............................
...............................

我们将使用randomForest()函数来创建决策树并查看它的图。
# Load the party package. It will automatically load other required packages.
library(party)
library(randomForest)
# Create the forest.
output.forest <- randomForest(nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
# View the forest results.
print(output.forest)
# Importance of each predictor.
print(importance(output.forest,type = 2))
当我们执行上面的代码,它产生以下结果 :
Call:
randomForest(formula = nativeSpeaker ~ age + shoeSize + score,
data = readingSkills)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 1
OOB estimate of error rate: 1%
Confusion matrix:
no yes class.error
no 99 1 0.01
yes 1 99 0.01
MeanDecreaseGini
age 13.95406
shoeSize 18.91006
score 56.73051
根据生成的随机森林中不同的树绘制误差率:
plot(output.forest)
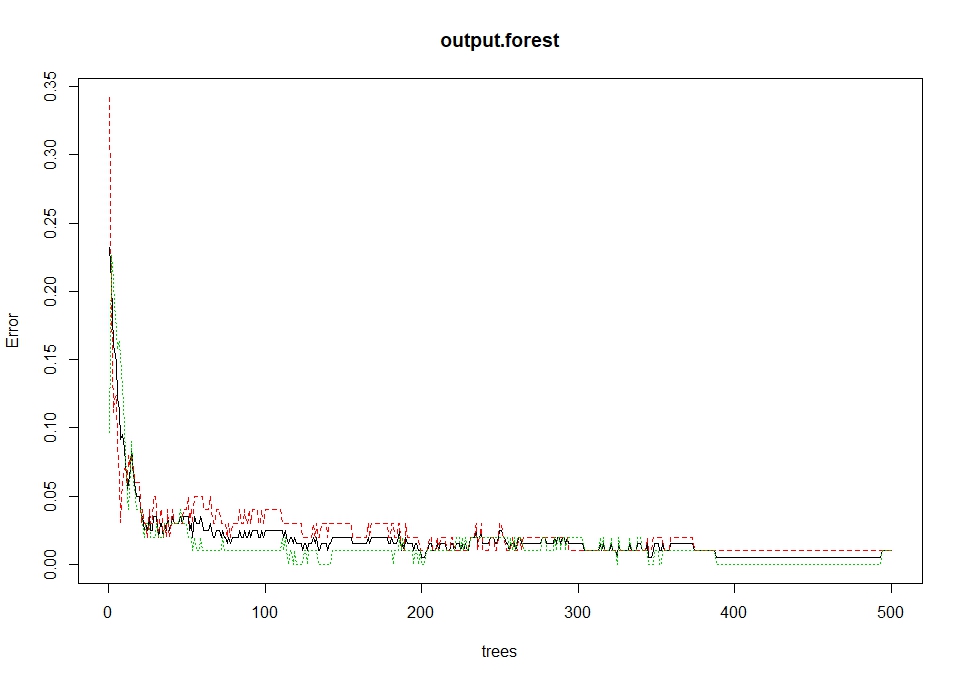
结论
从上面显示的随机森林,我们可以得出结论,鞋码和成绩是决定如果某人是母语者或不是母语的重要因素。 此外,该模型只有1%的误差,这意味着我们可以预测精度为99%。
四 常见问题
- 随机森林的随机体现在哪里? 随机森林的有两处随机的地方,第一是每棵树的训练样本是随机的,第二是每个节点的分裂属性也是随机选择的。两个随机性的引入,使得随机森林不容易过拟合。
随机森林中各个参数对模型的影响?
深度
深度越小,计算量越小,速度越快。
- 在特征不太容易互相影响的情况下,适当减少深度对结果无碍。
数据不够多的情况下似乎可以降低overfitting(?欢迎指正)
每棵树最大特征数(max_features)
一般用sqrt(总特征数),偶尔用log。总特征数越少,计算速度越快
你还知道别的集成学习吗?集成方式是什么
集成学习在各个规模的数据集上都有很好的策略。数据集大:划分成多个小数据集,学习多个模型进行组合。数据集小:利用Bootstrap方法进行抽样,得到多个数据集,分别训练多个模型再进行组合
集成学习常见有三类:Bagging,Boosting以及Stacking。在Bagging方法中,利用bootstrap方法从整体数据集中采取有放回抽样得到N个数据集,在每个数据集上学习出一个模型,最后的预测结果利用N个模型的输出得到,具体地:分类问题采用N个模型预测投票的方式,回归问题采用N个模型预测平均的方式。
提升方法(Boosting)是一种可以用来减小监督学习中偏差的机器学习算法。主要也是学习一系列弱分类器,并将其组合为一个强分类器。
Stacking方法是指训练一个模型用于组合其他各个模型。首先我们先训练多个不同的模型,然后把之前训练的各个模型的输出为输入来训练一个模型,以得到一个最终的输出。理论上,Stacking可以表示上面提到的两种Ensemble方法,只要我们采用合适的模型组合策略即可。但在实际中,我们通常使用logistic回归作为组合策略。