决策树分类实验
一 实验目的
- 了解决策树算法的原理，学会特征选择，分枝过程
- 了解决策树算法的实现过程，能比较多种不同决策树
- 学会使用R语言建立决策树分类模型
二 实验原理
决策树学习是一种逼近离散值目标函数的方法。通过将一组数据中学习的函数表示为决策树，从而将大量数据有目的的分类，从而找到潜在有价值的信息。决策树分类通常分为两步---生成树和剪枝；
树的生成：自上而下的递归分治法
剪枝：减去那些可能增大错误预测率的分支
决策树的方法起源于概念学习系统CLS（Concept Learning System）, 然后发展最具有代表性的ID3（以信息熵作为目标评价函数）算法，最后又演化为C4.5, C5.0,可以处理连续属性。
决策树的结构
以下面一个简单的用于是否买电脑预测的决策树为例子，树中的内部节点表示某个属性，节点引出的分支表示此属性的所有可能的值，叶子节点表示最终的判断结果也就是类型。
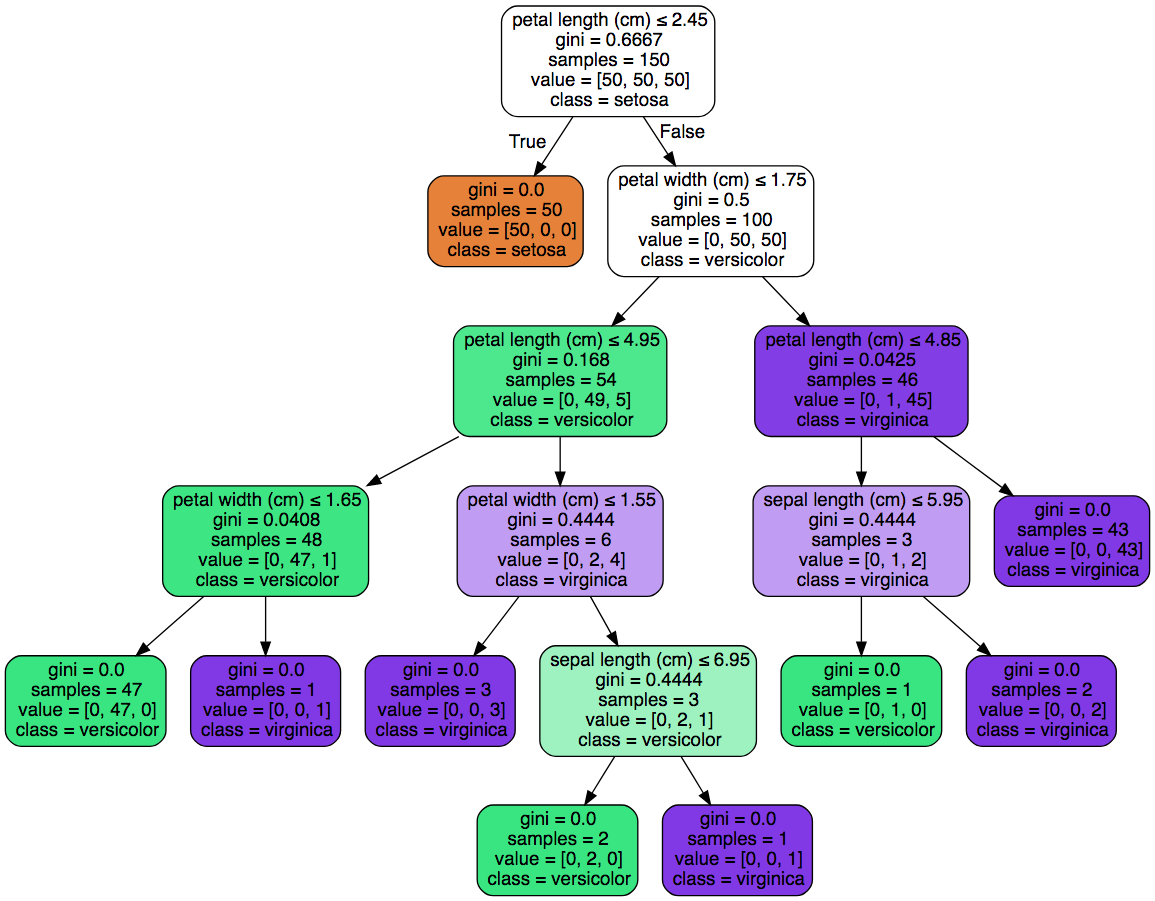
借助可视化工具例如Graphviz，matplotlib的注解等等都可以讲我们创建的决策树模型可视化并直接被人理解，这是贝叶斯神经网络等算法没有的特性。
决策树算法
决策树算法主要是指决策树进行创建中进行树分裂(划分数据集)的时候选取最优特征的算法，他的主要目的就是要选取一个特征能够将分开的数据集尽量的规整，也就是尽可能的纯. 最大的原则就是: 将无序的数据变得更加有序！这里总结以下三个常用的方法：
- 信息增益（imformation gain）
- 增益比率（gain ratio）
- 基尼不纯度（Gini impurity）
信息增益
信息论中告诉我们某个事件的信息量为这个事件发生的概率的负对数。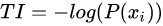
信息熵就是平均而言一个事件发生得到的信息量大小，也就是信息量的期望值.
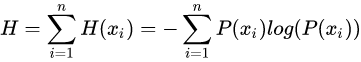
我们将一组数据集进行划分后，数据的信息熵会发生改变，我们可以通过使用信息熵的计算公式分别计算被划分的子数据集的信息熵并计算他们的平均值(期望值)来作为分割后的数据集的信息熵。新的信息熵的相比未划分数据的信息熵的减小值便是信息增益了.假设我们将数据集D划分成k份D1,D2,…,Dk，则划分后的信息熵为: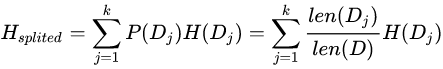
信息增益便是两个信息熵的差值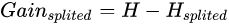
增益比率
增益比率是信息增益方法的一种扩展，是为了克服信息增益带来的弱泛化的缺陷。因为按照信息增益选择，总是会倾向于选择分支多的属性，这样会是的每个子集的信息熵最小。例如给每个数据添加一个第一无二的id值特征，则按照这个id值进行分类是获得信息增益最大的，这样每个子集中的信息熵都为0，但是这样的分类便没有任何意义，没有任何泛化能力，类似过拟合。
因此我们可以通过引入一个分裂信息来找到一个更合适的衡量数据划分的标准，即增益比率。
分裂信息的公式表示为: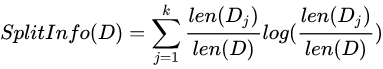
可见如果数据分的越多，分裂信息的值就会越大。这时候把分裂信息的值放到分母上便会中和信息增益带来的弊端。
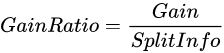
基尼不纯度
基尼不纯度的定义: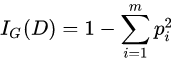 
其中m表示数据集D中类别的个数, pi表示某种类型出现的概率。可见当只有一种类型的时候基尼不纯度的值为0，此时不纯度最低。
针对划分成k个子数据集的数据集的基尼不纯度可以通过如下式子计算: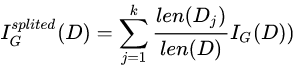
由此我们可以根据不纯度的变化来选取最有的树分裂属性
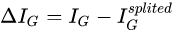
树分裂
有了选取最佳分裂属性的算法，下面我们就需要根据选择的属性来将树进一步的分裂。所谓树分裂只不过是根据选择的属性将数据集划分，然后在总划分出来的数据集中再次调用选取属性的方法选取子数据集的中属性。实现的最好方式就是递归了.
树分裂的终止条件有两个：
一个是遍历完所有的属性 可以看到，在进行树分裂的时候，我们的数据集中的数据向量的长度是不断缩短的，当缩短到0时，说明数据集已经将所有的属性用尽，便也分裂不下去了, 这时我们选取最终子数据集中的众数作为最终的分类结果放到叶子节点上.
另一个是新划分的数据集中只有一个类型。 若某个节点所指向的数据集都是同一种类型，那自然没有必要在分裂下去了即使属性还没有遍历完.
三 实验步骤
- 我们使用rpart包来实现决策树分类： 加载rpart包
#安装本次试验需要的R包
install.packages("rpart")
install.packages("rpart.plot")
install.packages("pROC")
- 我们依然使用经典的iris数据集来做我们的决策树分类实验：
>str(iris)
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
- 划分训练集和测试集：
set.seed(100)
samples<-sample(c(0,1),nrow(iris),replace = T,prob = c(0.8,0.2))
train<-iris[samples==0,]
test <-iris[samples==1,]
- 用训练集建模，观察模型结果：
library(rpart)
tree.both<-rpart(Species~.,data=iris,method = "class")
summary(tree.both)
#查看重要性
tree.both$variable.importance
#结果为
Petal.Width Petal.Length Sepal.Length Sepal.Width
88.96940 81.34496 54.09606 36.01309
- 画决策树：有两种画法，第一种比较简单，第二种通过使用rpart的扩展包plot画出更好看的决策树
plot(tree.both)
text(tree.both,use.n = T,all=T,cex=0.9)
library(rpart.plot)
rpart.plot(tree.both,branch=1,shadow.col = "gray",box.col="green",border.col="blue",split.col="red",main="design tree")
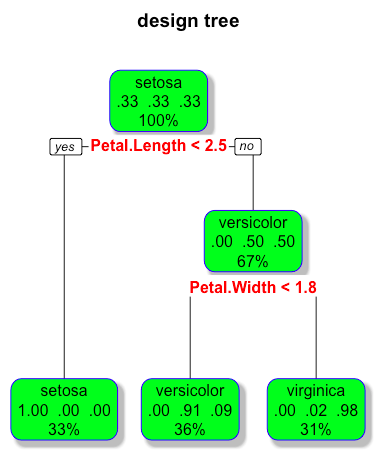
- 在测试集上做预测
library(pROC)
pred.tree.both<-predict(tree.both,newdata=test)
#查看预测结
pred.tree.both